
【题目】现有一笔直的公路连接![]() 、
、![]() 两地,甲车从
两地,甲车从![]() 地驶往
地驶往![]() 地,速度为每小时60千米,同时乙车从
地,速度为每小时60千米,同时乙车从![]() 地驶往
地驶往![]() 地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往
地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往![]() 地.设甲车行驶的时间为
地.设甲车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() .已知
.已知![]() 与
与![]() 的函数关系的部分图像如图所示.
的函数关系的部分图像如图所示.
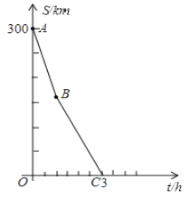
(1)直接写出![]() 点的实际意义.
点的实际意义.
(2)问:甲车出发几小时后发生故障?
(3)将![]() 与
与![]() 的函数图象补充完整.(请对画出的图象用数据作适当的标注)
的函数图象补充完整.(请对画出的图象用数据作适当的标注)
【答案】(1)是甲车故障开始修理了,乙车还在继续行驶;(2)1小时;(3)见解析
【解析】
(1)B点开始两车距离变化变慢,说明甲车故障开始修理了;
(2)根据图象,3小时时两车相遇,再求出相遇时甲车行驶的路程,然后根据时间=路程÷速度计算即可得解;
(3)根据两车行驶的情况分类讨论.
解:(1)点![]() 的实际意义是甲车故障开始修理了,乙车还在继续行驶;
的实际意义是甲车故障开始修理了,乙车还在继续行驶;
(2)t=3时,两车距离为0km,两车相遇,
∵80×3=240km,
∴发生故障前甲车行驶路程为300-240=60km,
时间位:60÷60=1小时;
∴甲车出发1小时后发生故障.
(3)甲车再次行驶时,t=1+2.5=3.5h,
乙车到达N地时,t=300÷80=3.75h,
甲车到达M地时,t=300÷60+2.5=7.5h,
所以,3<t≤3.5时,s=80(t-3)=80t-240,
t=3.5时,80t-240=80×3.5-240=40km,
3.5<t≤3.75时,s=80(t-3)+60(t-3.5)=140t-450,
t=3.75时,140t-450=140×3.75-450=75km,
3.75<t≤7.5时,s=60(t-3.75)+75=60t-150
补全图形如图所示.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
(3)点G是抛物线上的动点,点F在x轴上的动点,若以A,C,F,G四个点为顶点的四边形是平行四边形,求出所有满足条件的点F坐标(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,线段
上,线段![]() 和
和![]() 之间的数量关系是 ,位置关系是 ;
之间的数量关系是 ,位置关系是 ;
(2)在(1)的条件下,当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,求证:
时,求证:![]() ;
;
(3)当点![]() 在线段
在线段![]() 的延长线上时,在线段
的延长线上时,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形:

(1)可知tanα=![]() ,tanβ=
,tanβ=![]() ,用“画图法”求tan(α+β)的值,具体解法如下:
,用“画图法”求tan(α+β)的值,具体解法如下:
第一步:如图1所示,构造符合题意两个“背靠背”的直角三角形;
第二步:如图2所示,将图1中所有数据同比例扩大3倍;
第三步:如图3所示,依托中间的Rt△ABD的各顶点构造“水平﹣﹣竖直辅助线”,构造出“一线三直角”基本相似型,并补成矩形ACEF;由图可知tan(α+β)= .
(2)依据(1)的方法,已知tanα=![]() ,tanβ=
,tanβ=![]() ,用“画图法”求tan(α+β)的值.
,用“画图法”求tan(α+β)的值.
(3)扩展延伸,已知tanα=![]() ,tanβ=
,tanβ=![]() ,直接写出tan(α﹣β)= .
,直接写出tan(α﹣β)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.
已知:△ABC.
求作:BC边上的高线.
作法:如图,
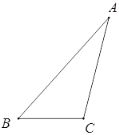
①以点C为圆心,CA为半径画弧;
②以点B为圆心,BA为半径画弧,两弧相交于点D;
③连接AD,交BC的延长线于点E.
所以线段AE就是所求作的BC边上的高线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵CA=CD,
∴点C在线段AD的垂直平分线上( ) (填推理的依据).
∵ = ,
∴点B在线段AD的垂直平分线上.
∴ BC是线段AD的垂直平分线.
∴AD⊥BC.
∴AE就是BC边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
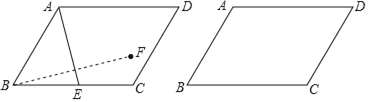
【题目】如图,已知ABCD中,∠ABC=60°,AB=4,BC=m,E为BC边上的动点,连结AE,作点B关于直线AE的对称点F.
(1)若m=6,①当点F恰好落在∠BCD的平分线上时,求BE的长;
②当E、C重合时,求点F到直线BC的距离;
(2)当点F到直线BC的距离d满足条件:2![]() ﹣2≤d≤2
﹣2≤d≤2![]() +4,求m的取值范围.
+4,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,若要使四边形EFGH为菱形,则还需增加的条件是( )
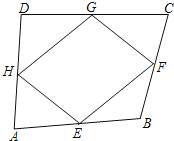
A.AC=BDB.AC⊥BDC.AC⊥BD且AC=BDD.AB=AD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com