
【题目】(1)解方程:![]() ;
;
(2)解不等式组: .
.
【答案】(1)x=4;(2)x<﹣8.
【解析】
(1)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论;
(2)一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
(1)去分母,得1﹣x=﹣1﹣2(x﹣3),
去括号,得1﹣x=﹣1﹣2x+6,
解得:x=4,
x=4时,分母x﹣3≠0,
故原分式方程的解为x=4;
(2)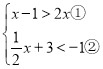
解不等式①,得 x<﹣1,
解不等式②,得 x<﹣8,
所以原不等式组的解集为x<﹣8.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
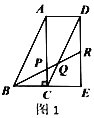
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() ,易得
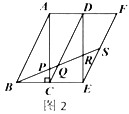
,易得![]() .若取四个直角三角形拼成如图2所示的形状,
.若取四个直角三角形拼成如图2所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
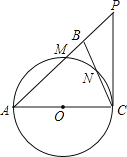
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
(3)在第(2)的条件下,求△ACP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后2分钟内,两人相遇的次数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一笔直的公路连接![]() 、
、![]() 两地,甲车从
两地,甲车从![]() 地驶往
地驶往![]() 地,速度为每小时60千米,同时乙车从
地,速度为每小时60千米,同时乙车从![]() 地驶往
地驶往![]() 地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往
地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往![]() 地.设甲车行驶的时间为
地.设甲车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() .已知
.已知![]() 与
与![]() 的函数关系的部分图像如图所示.
的函数关系的部分图像如图所示.
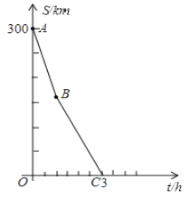
(1)直接写出![]() 点的实际意义.
点的实际意义.
(2)问:甲车出发几小时后发生故障?
(3)将![]() 与
与![]() 的函数图象补充完整.(请对画出的图象用数据作适当的标注)
的函数图象补充完整.(请对画出的图象用数据作适当的标注)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店因为经营不善欠下38000元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息)已知该店代理的某品牌服装的进价为每件40元,该品牌服装日的售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)当销售价为多少元时,该店的日销售利润最大;
(3)该店每天支付工资和其它费用共250元,该店能否在一年内还清所有债务.
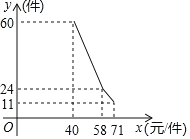
查看答案和解析>>
科目:初中数学 来源: 题型:
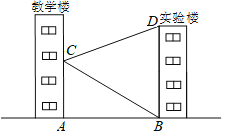
【题目】如图,学校教学楼对面是一幢实验楼,小朱在教学楼的窗口C测得实验楼顶部D的仰角为20°,实验楼底部B的俯角为30°,量得教学楼与实验楼之间的距离AB=30m.求实验楼的高BD.(结果精确到1m.参考数据tan20°≈0.36,sin20°≈0.34,cos20°≈0.94,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() (不经过点
(不经过点![]() 或点
或点![]() ),点
),点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
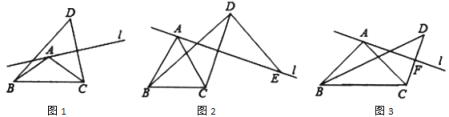
(1)如图1,根据已知可以判断点![]() 在以点
在以点![]() 为圆心,
为圆心,![]() 为半径的圆上.请你直接写出
为半径的圆上.请你直接写出![]() 的度数(用含
的度数(用含![]() 的式子表示).
的式子表示).
(2)如图2,当![]() 时,过点
时,过点![]() 作
作![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,当![]() 时,记直线
时,记直线![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() .将直线
.将直线![]() 绕点
绕点![]() 旋转,当线段
旋转,当线段![]() 的长取得最大值时,直接写出
的长取得最大值时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2019大洋湾盐城马拉松”的赛事共有三项:A,“全程马拉松”、B,“半程马拉松”、C.“迷你健身跑”,小明和小刚参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你健身跑”项目组的概率为 ;
(2)求小明和小刚被分配到不同项目组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com