
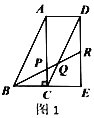
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() ,易得
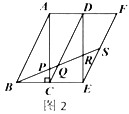
,易得![]() .若取四个直角三角形拼成如图2所示的形状,
.若取四个直角三角形拼成如图2所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】![]()
【解析】
首先证明△BCQ∽△BES,从而可求得CQ=![]() EF,DQ=
EF,DQ=![]() EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2.
EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2.
解:(1)∵四个直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴△BCQ∽△BES.
又∵BC=CE
∴CQ=![]() SE=
SE=![]() EF,
EF,
∴DQ=![]() EF,
EF,
∵AB∥CD,
∴∠ABP=∠DQR.
又∵∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
故答案为:4:1:3:2


科目:初中数学 来源: 题型:
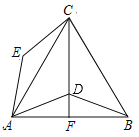
【题目】如图,点D是等边△ABC内一点,将线段AD绕着点A逆时针旋转60°得到线段AE,连结CD并延长交AB于点F,连结BD,CE.
(1)求证:△ACE≌△ABD;
(2)当CF⊥AB时,∠ADB=140°,求∠ECD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
(3)点G是抛物线上的动点,点F在x轴上的动点,若以A,C,F,G四个点为顶点的四边形是平行四边形,求出所有满足条件的点F坐标(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
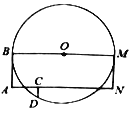
【题目】如图,![]() 是
是![]() 的直径,四边形
的直径,四边形![]() 是矩形,
是矩形,![]() 是
是![]() 上的点,
上的点,![]() ,与
,与![]() 交于点
交于点![]() ,己知
,己知![]() ,
,![]() 的半径为30.
的半径为30.
(1)求![]() 的长.
的长.
(2)连接![]() ,若将扇形
,若将扇形![]() 卷成一个圆锥,求这个圆锥底面半径的长.
卷成一个圆锥,求这个圆锥底面半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“江山如此多娇”为主题的地理知识竞赛活动,要求每班派出一名同学代表本班参赛.九年一班四名同学主动报名,老师为了确定最终参赛人选,对这四名同学的历次地理考试成绩进行了汇总,数据如下:

班级里数学小组的同学对上面的数据进行了进一步的整理:

根据以上的信息,回答下列问题:
(1)写出上表中![]() ,
,![]() ,
,![]() .
.
(2)丙同学看到统计表,对老师说:“我的成绩方差最小,说明我的成绩最稳定,应该派我去参赛!”请问你是否同意他的观点?若你是老师,你将派谁参赛?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市“上品”房地产开发公司于2010年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元![]() ,7月的销售单价为0.72万元
,7月的销售单价为0.72万元![]() ,且每月销售价格
,且每月销售价格![]() (单位:万元
(单位:万元![]() )与月份
)与月份![]() (
(![]() ,
,![]() 为整数)之间满足一次函数关系:每月的销售面积为
为整数)之间满足一次函数关系:每月的销售面积为![]() (单位:
(单位:![]() ),其中
),其中![]() .(
.(![]() ,
,![]() 为整数).
为整数).
(1)求![]() 与月份
与月份![]() 的函数关系式;
的函数关系式;
(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2010年11月时,因会受到即将实行的“国八条”和房产税政策的影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少![]() ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加![]() ,该计划顺利完成.为了尽快收回资金,2011年月公司进行降价促销,该月销售额为
,该计划顺利完成.为了尽快收回资金,2011年月公司进行降价促销,该月销售额为![]() 万元.这样12月、1月的销售额共为4618.4万元,请根据以上条件求出
万元.这样12月、1月的销售额共为4618.4万元,请根据以上条件求出![]() 的值为多少?
的值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com