
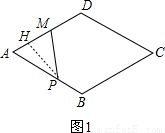
如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )





A B C D
A
【解析】
试题分析:分类讨论:当0≤x≤2,如图1,作PH⊥AD于H,AP=x,根据菱形的性质得∠A=60°,AM=2,则∠APH=30°,根据含30度的直角三角形三边的关系得到在RtAH=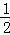 x,PH=
x,PH=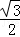 x,然后根据三角形面积公式得y=
x,然后根据三角形面积公式得y=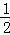 AM•PH=
AM•PH=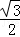 x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=2,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=
x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=2,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=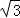 ,然后根据三角形面积公式得y=
,然后根据三角形面积公式得y=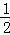 AM•BE=
AM•BE=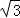 ;
;
当4<x≤6,如图3,作PF⊥AD于F,AB+BC+PC=x,则PD=6﹣x,根据菱形的性质得∠ADC=120°,则∠DPF=30°,在Rt△DPF中,根据含30度的直角三角形三边的关系得DF=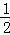 (6﹣x),PF=
(6﹣x),PF=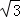 DF=
DF= (6﹣x),则利用三角形面积公式得y=
(6﹣x),则利用三角形面积公式得y=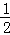 AM•PF=﹣
AM•PF=﹣ x+3
x+3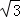 ,最后根据三个解析式和对应的取值范围对各选项进行判断.
,最后根据三个解析式和对应的取值范围对各选项进行判断.
【解析】
当点P在AB上运动时,即0≤x≤2,如图1,
作PH⊥AD于H,AP=x,
∵菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,
∴∠A=60°,AM=2,
∴∠APH=30°,
在Rt△APH中,AH=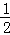 AP=
AP=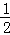 x,
x,
PH=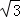 AH=
AH= x,
x,
∴y= AM•PH=
AM•PH= •2•
•2•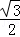 x=
x=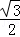 x;
x;
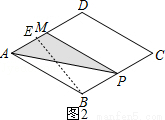
当点P在BC上运动时,即2<x≤4,如图2,
作BE⊥AD于E,AP+BP=x,
∵四边形ABCD为菱形,∠B=120°,
∴∠A=60°,AM=2,AB=2,BC∥AD,
∴∠ABE=30°,
在Rt△ABE中,AE= AB=1,
AB=1,
PH=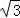 AE=
AE=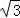 ,
,
∴y= AM•BE=
AM•BE= •2•
•2•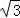 =
= ;
;
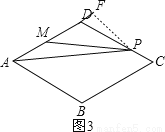
当点P在CD上运动时,即4<x≤6,如图3,
作PF⊥AD于F,AB+BC+PC=x,则PD=6﹣x,
∵菱形ABCD中,∠B=120°,
∴∠ADC=120°,
∴∠DPF=30°,
在Rt△DPF中,DF= DP=
DP= (6﹣x),
(6﹣x),
PF= DF=
DF= (6﹣x),
(6﹣x),
∴y= AM•PF=
AM•PF= •2•
•2• (6﹣x)=
(6﹣x)=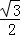 (6﹣x)=﹣
(6﹣x)=﹣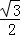 x+3
x+3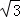 ,
,
∴△APM的面积y与点P经过的路程x之间的函数关系的图象为三段:当0≤x≤2,图象为线段,满足解析式y=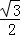 x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为
x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为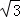 ;当4≤x≤6,图象为线段,且满足解析式y=﹣
;当4≤x≤6,图象为线段,且满足解析式y=﹣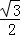 x+3
x+3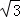 .
.
故选A.
考点:动点问题的函数图象


科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:填空题
将两个形状相同的三角板放置在一张矩形纸片上,按图示画线得到四边形ABCD,则四边形ABCD的形状是 .

查看答案和解析>>
科目:初中数学 来源:2015届北京市丰台区八年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,在梯形ABCD中,AD∥BC,如果∠ABC=60º,BD平分∠ABC,且BD⊥DC,CD=4, 那么梯形ABCD的周长是 .

查看答案和解析>>
科目:初中数学 来源:2015届北京市丰台区八年级下学期期末考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,点A(1,2)关于x轴对称的点的坐标是( )
A.(1,2) B.(1,-2) C.(-1,2) D.(-1,-2)
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:解答题
在图中,画出△ABC关于 轴对称的△A1B1C1,写出△ABC关于
轴对称的△A1B1C1,写出△ABC关于 轴对称的△A2B2C2的各点坐标.
轴对称的△A2B2C2的各点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com