
分析 (1)先令x=0,求出点A坐标,再令y=0求出方程的根,分两种情况得出点B,C坐标;
(2)先判断得出点B,C坐标,再求出AB2,BC2,AC2,用m的范围得出AB,BC,AC的大小,从而得出结论;
(3)根据三角形的边角的不等关系得出结论.
解答 解:(1)令x=0,由y=x2+(2-m)x-2m(m≠2),
∴y=-2m,
∴A的坐标为(0,-2m)
令y=0,由y=x2+(2-m)x-2m(m≠2),
∴x2+(2-m)x-2m=0,
∴(x+2)(x-m)=0
∴x1 =-2,x2=m
∵B点在C点左边.
∴①当 m<-2时,B,C的坐标分别为(m,0)和(-2,0).
②当 m>-2,但m≠2时,B,C的坐标分别为(-2,0)和(m,0).
(2)不存在,
理由:∵m=a2-2a+4=(a-1)2+3≥3.
由(1)的结论知,A的坐标为(0,-2m),B,C的坐标分别为(-2,0)和(m,0).
∴AB2=4m2+4
BC2=(m+2)2=m2+4m+4
AC2=m2+4m2 =5m2
∵m≥3,
∴3m2=m×3m≥9m>4m,
∴AB2 =4m2+4>m2 +4m+4=BC2,
∴AB>BC.
∵m≥3,
∴m2>=9>4,
∴AC2 =5m2 >4m2 +4=AB2,
∴AC>AB.
∴AC>AB>BC.
∵AB2 +BC2=5m2+4m+8>5m2 =AC2.
∴不存在实数a,使△ABC为Rt△.
(3)不存在,
理由:∵m=a2-2a+4=(a-1)2+3≥3.
由(2)的结论知,AC>AB>BC.
∴∠BAC 最小.
∴不存在实数a,能使得∠BAC最大.
点评 此题是二次函数综合题,主要考查了坐标轴上点的特点,二次函数的极值,直角三角形的判断,三角形边的大小的判断方法,解本题的关键是得出AC>AB>BC.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
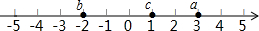 如图,数轴上有3个点,它们所表示的数分别用a,b,c.
如图,数轴上有3个点,它们所表示的数分别用a,b,c.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
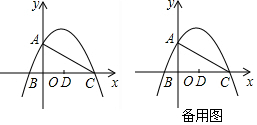
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A点传达到d3的不同途径中,经过站点b3的概率为( )
如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A点传达到d3的不同途径中,经过站点b3的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点P为反比例函数y=$\frac{{k}_{1}}{x}$上一点,向x,y轴上作垂线,交反比例函数y=$\frac{{k}_{2}}{x}$上于点A,B,交x轴于点D,交y轴于点C,则
点P为反比例函数y=$\frac{{k}_{1}}{x}$上一点,向x,y轴上作垂线,交反比例函数y=$\frac{{k}_{2}}{x}$上于点A,B,交x轴于点D,交y轴于点C,则查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | -$\sqrt{9}$=-3 | C. | (-$\sqrt{2}$)2=4 | D. | $\sqrt{48}$-$\sqrt{3}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知长方形ABCO,A,C分别在x轴、y轴上,O是原点,点B(2,1),点D($\sqrt{3}$,0),将四边形ABCD沿折痕CD翻折.
已知长方形ABCO,A,C分别在x轴、y轴上,O是原点,点B(2,1),点D($\sqrt{3}$,0),将四边形ABCD沿折痕CD翻折.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com