
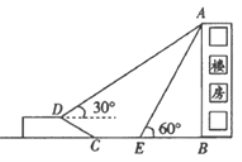
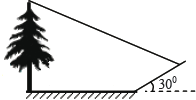
����Ŀ����ͼ����һ���ۺ�ʵ����У�С��Ҫ����һ¥���ĸ߶ȣ���������D�����¥������A������Ϊ300 ,�����������ߵ��½�C����Ȼ���ڵ�������CB��¥�������������10����E�������¥������A������Ϊ600 .��֪����CD=10�ף�ɽ�µ��¶�![]() (�¶� ��ָ�����Ǧֱ�߶���ˮƽ���ȵı�)��
(�¶� ��ָ�����Ǧֱ�߶���ˮƽ���ȵı�)��
(1)���D�����߶�(����D��ֱ��BC�ľ���);
(2)��¥��AB�߶�.(���������ʽ)
���𰸡���1��5�ף���2��(![]() )��.
)��.
��������
(1)����D��DM��BC������Ϊ��M����![]() ���ã�DM��CM��DC=
���ã�DM��CM��DC=![]() ��2�����ɵõ��𰸣�
��2�����ɵõ��𰸣�
(2)����D��DN��AB������ΪN����AB=x����BE=![]() ��AN=x-5��DN=10+5
��AN=x-5��DN=10+5![]() +
+![]() ������tan30��=
������tan30��=![]() ���г����̣��������.
���г����̣��������.
��1������D��DM��BC��������M��
��ɽ�µ��¶�![]() ��
��
��DM��CM��DC=![]() ��2��
��2��
��CD=10��
��DM=5��
���D�����߶���5��.
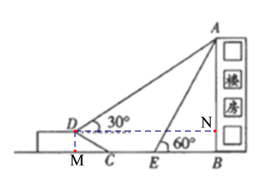
��2������D��DN��AB������ΪN��
��(1)���֪��DM=5��CM=5![]() ��
��
��CE=10��
��ME=10+5![]() ��
��
��AB=x����BE=![]() ��AN=x-5��
��AN=x-5��
��DN=MB=10+5![]() +
+![]() ��
��
��tan30��=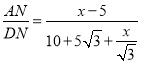 ��
��
�� 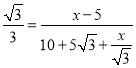 ����ã�x=
����ã�x=![]() ��
��
��¥��AB�߶���(![]() )��.
)��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BDΪ��ABC���Բ��O��ֱ�����ҡ�BAE����C��
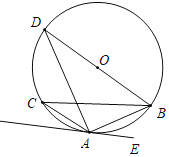
��1����֤��AE���O�����ڵ�A��
��2����AE��BC��BC��8��AB��2![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ȫУ![]() ��ѧ����У��ѧ�ķ�ʽ����ȫУ�����ȡ��������ѧ�������ʾ����飬�ʾ�������������ѧ��ʽ��ѧ��ѡ��ÿ�˱�ѡһ���ֻ��ѡһ��.���������������������ͳ��ͼ�ش��������⣺
��ѧ����У��ѧ�ķ�ʽ����ȫУ�����ȡ��������ѧ�������ʾ����飬�ʾ�������������ѧ��ʽ��ѧ��ѡ��ÿ�˱�ѡһ���ֻ��ѡһ��.���������������������ͳ��ͼ�ش��������⣺

��1������ε����У�����ȡ�˶�����ѧ����
��2����ȫ����ͳ��ͼ��
��3������ȫУ����ѧ�����ж����˳�����������ѧ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c������A��0����3����B����1��0����C��2����3������������x�����һ����Ϊ��E����PΪ��������һ���㣬���P�ĺ�����Ϊt��
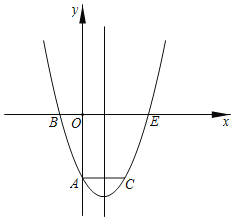
��1���������ߵĽ���ʽ��
��2������P�ڵ�һ���ޣ���MΪ�����߶Գ�����һ�㣬���ı���MBEPǡ����ƽ���ı���ʱ�����P�����ꣻ
��3������P�ڵ������ޣ�����PA��PE��AE����tΪ��ֵʱ����PAE���������������Ƕ��٣�
��4���Ƿ���ڵ�P��ʹ��PAEΪ��AEΪֱ�DZߵ�ֱ�������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() .
.
��1�����˺���ͼ����![]() ��ֻ��һ�����㣬��д��
��ֻ��һ�����㣬��д��![]() ��
��![]() ����Ĺ�ϵʽ.
����Ĺ�ϵʽ.
��2����![]() ����
����![]() ��
��![]() ��
��![]() �Ǹú���ͼ���ϵ�3���㣬�ԱȽ�
�Ǹú���ͼ���ϵ�3���㣬�ԱȽ�![]() ��
��![]() ��
��![]() �Ĵ�С.
�Ĵ�С.
��3����![]() ����
����![]() ʱ������
ʱ������![]() ��
��![]() �������������
�������������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
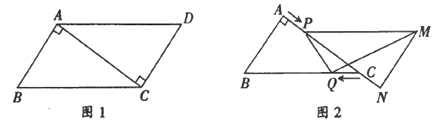
����Ŀ����ͼ1����ƽ���ı���ABCD�У�AB=3cm, BC=5cm, ![]() ,
, ![]() �� AC�ķ�������ƽ�Ƶõ�
�� AC�ķ�������ƽ�Ƶõ�![]() ���ٶ�Ϊ1 cm/ s;ͬʱ����Q�ӵ�C��������CB���������ƶ����ٶ�Ϊ1cm/s����
���ٶ�Ϊ1 cm/ s;ͬʱ����Q�ӵ�C��������CB���������ƶ����ٶ�Ϊ1cm/s����![]() ֹͣƽ��ʱ����QҲֹͣ�ƶ�����ͼ2�����ƶ�ʱ��Ϊt(s)(0< <4)������PQ,MQ ,
ֹͣƽ��ʱ����QҲֹͣ�ƶ�����ͼ2�����ƶ�ʱ��Ϊt(s)(0< <4)������PQ,MQ ,
�����������:
(1)��tΪ��ֵʱ��![]() ?
?
(2)��tΪ��ֵʱ��![]() ?
?
(3)��tΪ��ֵʱ��![]() ?
?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ���ɱ�Ϊÿ��30Ԫ����Ʒ���̵갴���۲����ڳɱ��ۣ��Ҳ�����50Ԫ���ۣ������鷢�֣�����Ʒÿ���������y�����������۵���x��Ԫ��֮������һ�κ�����ϵ����ͼ����ͼ��ʾ��
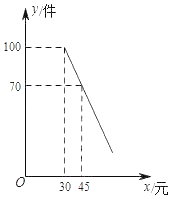
��1�������Ʒÿ���������y�����������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�����۵��۶�Ϊ����Ԫʱ������ʹ���۸���Ʒÿ���õ�����w��Ԫ�������������Ƕ��٣�
��3�����̵�Ҫʹ���۸���Ʒÿ���õ��������800Ԫ����ֱ��д��ÿ���������y��������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() �ڵ�һ����ͼ����ͼ��ʾ������A��1��0����x��Ĵ��ߣ�������������
�ڵ�һ����ͼ����ͼ��ʾ������A��1��0����x��Ĵ��ߣ�������������![]() ��ͼ���ڵ�M����AOM�����Ϊ3��
��ͼ���ڵ�M����AOM�����Ϊ3��

��1�����������Ľ���ʽ��
��2�����B������Ϊ��t��0��������t��1������ABΪһ�ߵ���������һ�������ڷ���������![]() ��ͼ���ϣ���t��ֵ��
��ͼ���ϣ���t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������һ�����ĸ߶ȣ�����������Ӱ��ǡ�����ڵ����һб���ϣ���ͼ����ʱ��õ����ϵ�Ӱ��Ϊ8���������ϵ�Ӱ��Ϊ4������֪б�µ��½�Ϊ300��ͬһʱ �̣�һ����Ϊl�ס���ֱ�ڵ�������ı���ڵ����ϵ�Ӱ��Ϊ2���������ĸ߶�Ϊ�� ��
A.![]() �� B.12�� C.
�� B.12�� C.![]() �� D��10��
�� D��10��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com