
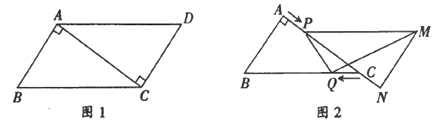
【题目】如图1,在平行四边形ABCD中,AB=3cm, BC=5cm, ![]() ,
, ![]() 沿 AC的方向匀速平移得到
沿 AC的方向匀速平移得到![]() ,速度为1 cm/ s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当
,速度为1 cm/ s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当![]() 停止平移时,点Q也停止移动,如图2,设移动时间为t(s)(0< <4),连结PQ,MQ ,
停止平移时,点Q也停止移动,如图2,设移动时间为t(s)(0< <4),连结PQ,MQ ,
解答下列问题:
(1)当t为何值时,![]() ?
?
(2)当t为何值时,![]() ?
?
(3)当t为何值时,![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意得:AP=t,CQ=t,CP=4-t,当![]() 时,则AB∥PQ,得到:
时,则AB∥PQ,得到:![]() ,即可求解;
,即可求解;
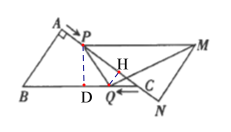
(2)过点Q作QH⊥AC于点H,易证:CQH~CBA,得QH=![]() ,CH=
,CH=![]() ,PH=4-
,PH=4-![]() ,当
,当![]() 时,则PQH为等腰直角三角形,列出方程,即可求解;
时,则PQH为等腰直角三角形,列出方程,即可求解;
(3)过点P作PD⊥BC,易证:PQD~ MPQ,得:![]() ,由PDC~BAC,得
,由PDC~BAC,得![]() ,
,![]() ,DQ =
,DQ =![]() ,结合
,结合![]() ,列出方程,即可求解.
,列出方程,即可求解.
(1)∵AB=3cm, BC=5cm, ![]() ,
,
∴AC=![]() ,
,
由题意得:AP=t,CQ=t,CP=4-t,
∵AB∥MN,
∴当![]() 时,则AB∥PQ,
时,则AB∥PQ,
∴![]() ,即:
,即:![]() ,解得:t=
,解得:t=![]() ;
;
∴当t =![]() 时,
时,![]() ;
;
(2)过点Q作QH⊥AC于点H,
∴QH∥BA,
∴CQH~CBA,
∴CQ:QH:CH=CB:BA:CA=5:3:4,
∴QH=![]() ,CH=
,CH=![]() ,
,
∴PH=4-t-![]() =4-
=4-![]() ,
,
当![]() 时,则PQH为等腰直角三角形,
时,则PQH为等腰直角三角形,
∴PH=QH,即:![]() =4-
=4-![]() ,解得:t=
,解得:t=![]() ,
,
∴当t=![]() 时,
时,![]() ;
;
(3)过点P作PD⊥BC,
若![]() ,则∠PQM=∠PDQ,
,则∠PQM=∠PDQ,
∵PM∥BC,
∴∠MPQ=∠PQD,
∴PQD~ MPQ,
∴![]() ,
,
∴![]() ,
,
∴ ![]() .
.
∵∠PDC=∠BAC=90°,∠ACB=∠DCP,
∴PDC~BAC,
∴![]() ,即:
,即:![]() ,
,
解得:![]() ,
,![]() ,
,
∴DQ=CD-CQ=![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),
(舍去),
∴当t=![]() 时,
时,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
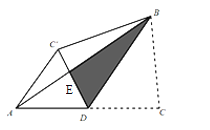
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
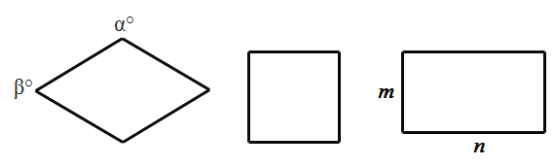
【题目】如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为![]() ,
,![]() ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为![]() ,于是
,于是![]() 越小,菱形越接近正方形.
越小,菱形越接近正方形.
①若菱形的一个内角为![]() ,则该菱形的“接近度”为_________;
,则该菱形的“接近度”为_________;
②当菱形的“接近度”等于_________时,菱形是正方形;
(2)设矩形的长和宽分别为![]() ,
,![]()
![]() ,试写出矩形的“接近度”的合理定义.
,试写出矩形的“接近度”的合理定义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量![]() 取
取![]() 时,函数值
时,函数值![]() 也等于
也等于![]() ,则称
,则称![]() 是这个函数的不动点.
是这个函数的不动点.
已知二次函数![]() .
.
(1)若3是此函数的不动点,则![]() 的值为__________.
的值为__________.
(2)若此函数有两个相异的不动点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
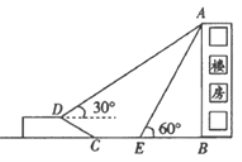
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为300 ,沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为600 .已知坡面CD=10米,山坡的坡度![]() (坡度 是指坡面的铅直高度与水平宽度的比),
(坡度 是指坡面的铅直高度与水平宽度的比),
(1)求点D离地面高度(即点D到直线BC的距离);
(2)求楼房AB高度.(结果保留根式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B=____.
(问题解决)
(3)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在七年级、八年级开展了阅读文学名著知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(单位:分),并对数据进行整理、描述和分析.下面给出了部分信息.
a.七年级学生知识竞赛成绩的平均数、中位数、众数、优秀率(80分及以上)如下表所示:
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 84. 2 | 77 | 74 | 45﹪ |
b.八年级学生知识竞赛成绩的扇形统计图如下(数据分为5组,A:50≤x≤59; B:60≤x≤69;C:70≤x≤79;D:80≤x≤89;E:90≤x≤100)
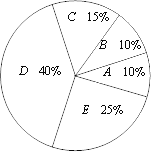
c.八年级学生知识竞赛成绩在D组的是:87 88 88 88 89 89 89 89
根据以上信息,回答下列问题:
(1)八年级学生知识竞赛成绩的中位数是 分;
(2)请你估计该校七、八年级所有学生中达到“优秀”的有多少人?
(3)下列结论:①八年级成绩的众数是89分;②八年级成绩的平均数可能为86分;③八年级成绩的极差可能为50分.其中所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.
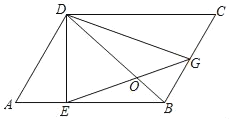
(1)求证:GD=EG.
(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.
(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时,![]() = ;
= ;
②当θ=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com