
【题目】不能够铺满地面的组合图形是( )
A. 正八边形和正方形 B. 正方形和正三角形
C. 正六边形和正方形 D. 正六边形和正三角形
【答案】C
【解析】
正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解:A、正八边形和正方形内角分别为135°、90°,由于135×2+90=360,故能铺满,不符合题意;;
B、正三角形和正方形内角分别为60°、90°,由于60×3+90×2=360,故能铺满,不符合题意;
C、正方形的每个内角是90°,正六边形的每个内角是120°,90m+120n=360°,m=4-![]()
n,显然n取任何正整数时,m不能得正整数,故不能够铺满,符合题意;
D、正六边形的每个内角是120°,正三角形的每个内角是60°,由于2×120°+2×60°=360°,或120°+4×60°=360°,故能够铺满,不符合题意;
故选:C.


科目:初中数学 来源: 题型:
【题目】化简或求值
(1)若A=-2a2+ab-b3,B=a2-2ab+b3,求A -2B的值。
(2)先化简,再求值:5x2y-3xy2-7(x2y- xy![]() ),其中x=2,y=-1。
),其中x=2,y=-1。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为 ![]() BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )![]()
A.点E
B.点F
C.点M
D.点N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 ![]() BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )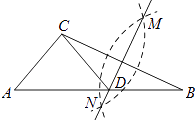
A.∠CAD=40°
B.∠ACD=70°
C.点D为△ABC的外心
D.∠ACB=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.
(1)在这个过程中,自变量是 ,因变量是 .
(2)景点离小明家多远?
(3)小明一家在景点游玩的时间是多少小时?
(4)小明到家的时间是几点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y= ![]() 在第一象限内的图象交于点P,则k=;△POA的面积为 .
在第一象限内的图象交于点P,则k=;△POA的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.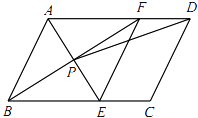
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,②一①得:3S﹣S=39﹣1,即2S=39﹣1,∴S= ![]() .得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 .
.得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com