
分析 方程的解就是能够使方程两边左右相等的未知数的值,即利用方程的解代替方程中的未知数,所得到的式子左右两边相等.
解答 解:(1)当x=1时,左边=2×1×(1+1)=4,右边=4×(1+1)=8,左边≠右边,1不是方程的解;
当x=-1时,左边=2×(-1)×(-1+1)=0,右边=4×(-1+1)=0,左边=右边,-1是方程的解;
当x=2时,左边=2×2×(2+1)=12,右边=4×(2+1)=12,左边=右边,2是方程的解;
当x=-2时,左边=2×(-2)×(-2+1)=4,右边=4×(-2+1)=-4,左边≠右边,-2不是方程的解;
(2)当x=1时,左边=12-1-2=-2,右边=0,左边≠右边,1不是方程的解;
当x=-1时,(-1)2-(-1)-2=0,右边=0,左边=右边,-1是方程的解;
当x=2时,左边=22-2-2=0,右边=0,左边=右边,2是方程的解;
当x=-2时,左边=(-2)2-(-2)-2=4,右边=0,左边≠右边,-2不是方程的解.
点评 本题考查了方程的解,检验一个数是否为相应的方程的解,就是把这个数代替方程中的未知数,看左右两边的值是否相等,如果左边=右边,那么这个数就是该方程的解;反之,这个数就不是该方程的解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
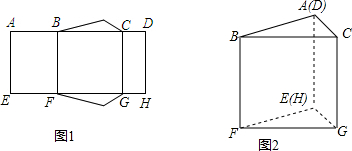
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
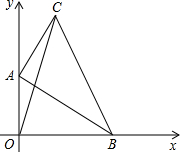 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )| A. | 5 | B. | 2+$\sqrt{13}$ | C. | $\sqrt{13}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\sqrt{x-1}(x≥1)$ | B. | y=-$\sqrt{x-1}(x≥1)$ | C. | y=$\sqrt{1-x}(x≤1)$ | D. | y=±$\sqrt{1-x}(x≤1)$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).
如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
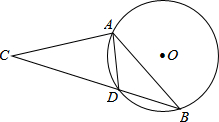 如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | 2 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com