
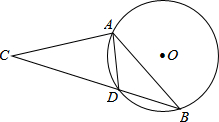
 如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | 2 | D. | $\sqrt{3}$+1 |
分析 利用圆周角定理确定点C的运动轨迹,进而利用点与圆的位置关系求得OC长度的取值范围.
解答 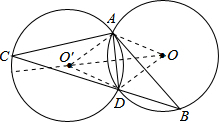 解:如图,连接OA、OD,则△OAD为等边三角形,边长为半径1.
解:如图,连接OA、OD,则△OAD为等边三角形,边长为半径1.
作点O关于AD的对称点O′,连接O′A、O′D,则△O′AD也是等边三角形,边长为半径1,
∴OO′=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$.
由题意可知,∠ACB=∠ABC=$\frac{1}{2}$∠AOD=30°,
∴∠ACB=$\frac{1}{2}$∠AO′D,
∴点C在半径为1的⊙O′上运动.
由图可知,OC长度的取值范围是:$\sqrt{3}$-1≤OC≤$\sqrt{3}$+1.
故选A.
点评 本题涉及圆的知识,难度较大.解题要点是确定点C的运动轨迹.


科目:初中数学 来源: 题型:填空题
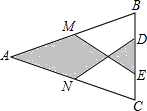 如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=4cm,则图中阴影部分的面积为$\frac{86}{3}$cm2.
如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=4cm,则图中阴影部分的面积为$\frac{86}{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+1-10-x=1 | B. | 4x+2-10+x=1 | C. | 4x+2-10-x=6 | D. | 4x+2-10+x=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com