
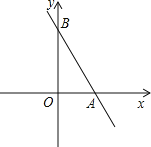
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 是
是![]() 轴上一点,若将
轴上一点,若将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴上,则点
轴上,则点![]() 的坐标为___________.
的坐标为___________.
【答案】(0,![]() )或(0,-
)或(0,-![]() )
)
【解析】
设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,则有AB=AC,而AB的长度根据已知可以求出,所以C点的坐标由此求出;又由于折叠得到CM=BM,在直角△CMO中根据勾股定理可以求出OM,也就求出M的坐标.注意分两种情况求解.
解:如图所示,当点M在y轴正半轴上时,设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,则有AB=AC,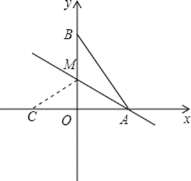
∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B,
轴分别交于点A、B,
∴A(5,0),B(0,12),
又OA=5,OB=12,
∴AB=13,
∴点C的坐标为:(-8,0).
再设M点坐标为(0,b),
则CM=BM=12-b,
∵CM2=CO2+OM2,
∴b=![]() ,
,
∴M(0,![]() ),
),
如图所示,当点M在y轴负半轴上时,设OM=m,
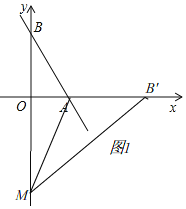
由折叠知,AB'=AB=13,B'M=BM,BM=OB+OM=12+m,
∴OB'=18,B'M=12+m
根据勾股定理得,![]() ,
,
∴m=![]() ,
,
∴M(0,-![]() )
)
故答案为:(0,![]() )或(0,-
)或(0,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,以![]() 的边
的边![]() 、
、![]() 为边的等边三角
为边的等边三角![]() 和等边三角形
和等边三角形![]() ,四边形
,四边形![]() 是平行四边形.
是平行四边形.
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形;
是矩形;
![]() 当
当![]() 满足什么条件时,平行四边形
满足什么条件时,平行四边形![]() 不存在;
不存在;
![]() 当
当![]() 分别满足什么条件时,平行四边形
分别满足什么条件时,平行四边形![]() 是菱形,正方形?
是菱形,正方形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
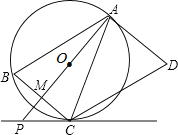
(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,D是![]() 中点,若∠BAC=70°,求∠C.
中点,若∠BAC=70°,求∠C.
下面是小雯的解法,请帮他补充完整.
解:在⊙O中,
∵D是![]() 的中点
的中点
∴![]() =
=![]() ,
,
∴∠l=∠2( )(填推理的依据)
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径,
∴∠ADB=90°( )(填推理的依据)
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上,
∴∠C+∠B=180°( )(填推理的依据)
∴∠C=l80°﹣∠B= (填计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=2,点C在![]() 上运动,且∠ACB=30°.
上运动,且∠ACB=30°.

(1)求⊙O的半径;
(2)设点C到直线AB的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
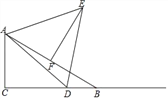
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在南开中学校庆78周年之际,由学生处和美术教研组共同策划、组织了“南开中学校园明信片设计大赛”。获得此次设计大赛组织一等奖的![]() 、
、![]() 、
、![]() 、
、![]() 四个班级一共有75件作品获奖,已知
四个班级一共有75件作品获奖,已知![]() 班参赛作品的获奖率为30%,
班参赛作品的获奖率为30%,![]() 班参赛作品的获奖率为40%。请结合两幅统计图所提供的信息,解决下列问题:
班参赛作品的获奖率为40%。请结合两幅统计图所提供的信息,解决下列问题: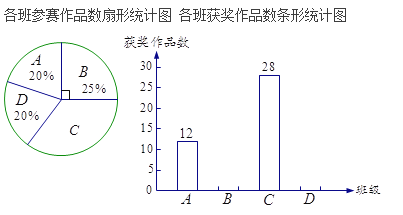
(1)四个班级一共选送了多少件作品参赛,获奖率最高的班级是哪个班;
(2)请将条形统计图补充完整;
(3)![]() 班的小欣和小怡同学在本次大赛中荣获个人一等奖,此外
班的小欣和小怡同学在本次大赛中荣获个人一等奖,此外![]() 、
、![]() 两班各有一名同学荣获个人一等奖。南开中学校友会准备从这4名同学的作品中任选两件,制作成新年贺卡送给老校友。请用列表法或画树状图的方法求出这两件作品分别来自不同班级,且其中一件是小欣或小怡作品的概率.
两班各有一名同学荣获个人一等奖。南开中学校友会准备从这4名同学的作品中任选两件,制作成新年贺卡送给老校友。请用列表法或画树状图的方法求出这两件作品分别来自不同班级,且其中一件是小欣或小怡作品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com