
【题目】在△ABC 中,AB BC AC,∠A ∠B ∠C 60°.点 D、E 分别是边 AC、AB 上的点(不与 A、B、C 重合),点 P 是平面内一动点.设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点 P 在边 BC 上运动(不与点 B 和点 C 重合),如图⑴所示,则∠1+∠2 .(用 α 的代数式表示)
(2)若点 P 在△ABC 的外部,如图⑵所示,则∠α、∠1、∠2 之间有何关系?写出你的结论,并说明理由.
(3)当点 P 在边 BC 的延长线上运动时,试画出相应图形,并写出∠α、∠1、∠2 之间的关系式.(不需要证明)

【答案】(1)如图(1)60 α ;(2)∠2=60 ∠1 α;理由见解析;(3)如图(3)时,2 1 60 α,如图(4)时,∠2 ∠1=60 α.
【解析】
(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用三角形内角和定理以及邻补角的性质可得出∠α=∠1-∠2+60°;
(3)利用三角外角的性质得出.需要分类讨论,如图所示.
(1)如图(1),∵∠1+∠2+∠ADP+∠AEP=360°,∠A+α+∠ADP+∠AEP=360°,
∴∠1+∠2=∠A+α,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠1+∠2=60°+α.
故答案是:60°+α;
(2)∠2=60 ∠1 α,
证明:如图(2),
∵ 1 是△POD 的外角,
∴∠1=α+∠POD,
∵∠POD=∠AOE,
∴∠1=α+∠AOE,
∴∠AOE=∠1,
∵∠2 是△AOE 的外角,
∴∠2=∠A ∠AOE,
∴∠2=60 ∠1 α;
(3)两种情况如下:
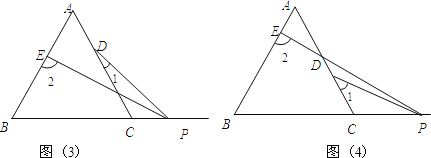
如图(3)时,2 1 60 α,
如图(4)时,∠2 ∠1=60 α.


科目:初中数学 来源: 题型:
【题目】如图,A,B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)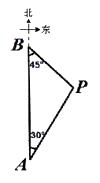
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)12016 +![]() 3.14 π 0
3.14 π 0
(2) 3a2 3 2a a5
(3) x 2 x 1 3xx 1
(4)2a b c2a b c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【问题提出】如图1.△ABC是等边三角形,点D在线段AB上.点E在直线BC上.且∠DEC=∠DCE.求证:BE=AD;
(2)【类比学习】如图2.将条件“点D在线段AB上”改为“点D在线段AB的延长线上”,其他条件不变.判断线段AB,BE,BD之间的数量关系,并说明理由.
(3)【扩展探究】如图3.△ABC是等腰三角形,AB=AC,∠BAC=120°,点D在线段AB的反向延长线上,点E在直线BC上,且∠DEC=∠DCE,【类比学习】中的线段AB、BE、BD之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出线段AB,BE,BD之间的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1 是一个长为 4a、宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图 2).
(1)图 2 中的阴影部分的面积为 ;(用 a、b 的代数式表示)
(2)观察图 2 请你写出a b2 、a b2 、ab 之间的等量关系是 ;
(3)根据⑵中的结论,若 x y 5 , x y ![]() ,则 x y2 =_______.
,则 x y2 =_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,
求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°(___________)
∴∠ADC=∠EGC(等量代换)
∴AD∥EG(_____________)
∴∠1=∠2(___________)
∠E=∠3(___________)
又∵∠E=∠1( 已知)
∴∠2=∠3(___________)
∴AD平分∠BAC(___________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com