
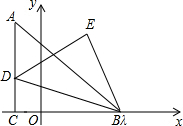
 已知Rt△ABC中,∠ACB=90°,AC=BC,且点B(a+1,0),C(b,0)都在平面直角坐标系的x轴上,如图所示,且满足a2+b2-10a+4b+29=0,点D为射线AC上一动点且纵坐标为m,以BD为斜边,按顺时针顺序作△BDE,使∠DEB=90°,EB=ED.
已知Rt△ABC中,∠ACB=90°,AC=BC,且点B(a+1,0),C(b,0)都在平面直角坐标系的x轴上,如图所示,且满足a2+b2-10a+4b+29=0,点D为射线AC上一动点且纵坐标为m,以BD为斜边,按顺时针顺序作△BDE,使∠DEB=90°,EB=ED.分析 (1)根据点B(a+1,0),C(b,0)都在平面直角坐标系的x轴上,且满足a2+b2-10a+4b+29=0,可求得a,b的值,从而求得点B、C的坐标;
(2)根据∠DEB=90°,EB=ED,点B的坐标为(6,0),点C的坐标为(-2,0),点D为射线AC上一动点且纵坐标为m,可以确定点D的坐标,然后作辅助线EG⊥x轴于点G,DF⊥EG于点F,然后根据题目中各点的坐标,设出点E的坐标(x,y),再根据图形和各点的坐标,列出方程组,从而得到用含m的式子表示表示点E的坐标;
(3)根据题目中的信息和第二问中求得的点E的坐标进行推导,可以得到使得EF=2CD时,点D的坐标.
解答 解:(1)∵a2+b2-10a+4b+29=0,
∴(a-5)2+(b+2)2=0.
∴a-5=0,b+2=0.
解得,a=5,b=-2.
∴点B的坐标为(6,0),点C的坐标为(-2,0).
(2)如下图所示:作EG⊥x轴于点G,DF⊥EG于点F.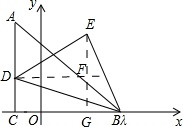
设点E的坐标为(x,y).
∵∠DEB=90°,EB=ED,点B的坐标为(6,0),点C的坐标为(-2,0),点D为射线AC上一动点且纵坐标为m,
∴点D的坐标为(-2,m).
∴∠EFD=∠BGF=90°,DE=BE,∠DEF=∠EBG.
∴△DEF≌△EBF.
∴EF=BG,BF=EG.
∴$\left\{\begin{array}{l}{x-(-2)=y}\\{y-m=6-x}\end{array}\right.$.
解得,$x=\frac{4+m}{2},y=\frac{8+m}{2}$.
故点E的坐标为($\frac{4+m}{2},\frac{8+m}{2}$).
(3)存在这样的点D,恰使EF=2CD.
第一种情况:当点D在x轴上方时,如下图所示:取AD的中点F,连接EF,作EG⊥AD于点G.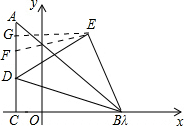
∵点A的坐标为(-2,8),点D的坐标为(-2,m),点E的坐标为($\frac{4+m}{2},\frac{8+m}{2}$),点C的坐标为(-2,0),
∴CD=m,GE=$\frac{4+m}{2}-(-2)$=$\frac{8+m}{2}$,GF=$\frac{8+m}{2}-(\frac{8-m}{2}+m)=0$.
∴此时GE与EF重合,EF=GE=$\frac{8+m}{2}$.
∵EF=2CD,
∴$\frac{8+m}{2}=2m$.
解得,m=$\frac{8}{3}$.
∴点D的坐标为(-2,$\frac{8}{3}$).
第二种情况:当点D在x轴下方时,如下图所示: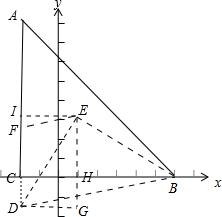
作EI⊥AC于点I,EH⊥x轴于点H,DG⊥EH交EH的延长线于点G,
∵点A的坐标为(-2,8),点D的坐标为(-2,m),点C的坐标为(-2,0),点F为AD的中点,
∴点F的坐标为(-2,$\frac{8+m}{2}$).
设E点的坐标为(x,y),
∵EB=ED,∠EID=∠EGD=∠EHB=90°,
∴△EID≌△EGD≌△EHB.
∴EI=EH,DI=BH.
又∵EF=2CD,
∴$\left\{\begin{array}{l}{x-(-2)=y}\\{y-m=6-x}\\{-2m=\sqrt{(x+2)^{2}+(y-\frac{8-m}{2})^{2}}}\end{array}\right.$
解得,x=1.2,y=3.2,m=-1.6.
∴点D的坐标为:(-2,-1.6).
点评 本题考查根据关系式求值的问题,可以根据题目中的信息,用代数式表示别的量的知识,根据题目中的信息进行探索结论的相关知识,关键是根据题目中的信息画出符合要求的图形,然后根据题目中的信息结合图形进行正确分析,进而求得所要解答的问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
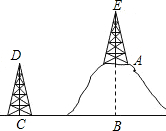 如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?
如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
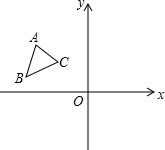 如图,△ABC中,A(-2,3),B(-3,1),C(-1,2).
如图,△ABC中,A(-2,3),B(-3,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A市 | B市 | C市 | |
| D市 | 200元/台 | 300元/台 | 400元/台 |
| E市 | 800元/台 | 700元/台 | 500元/台 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com