
【题目】如图,AB为圆O的直径,PD切圆O于点C,交AB的延长线于点D,且 ![]() D=2
D=2 ![]() CAD.
CAD.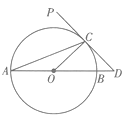
(1)求 ![]() D的度数;
D的度数;
(2)若CD=2,求BD的长.
【答案】
(1)解:∵ ![]() 和
和 ![]() 分别是弧
分别是弧 ![]() 所对的圆心角和圆周角,∴
所对的圆心角和圆周角,∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∵ ![]() 与⊙O相切于点
与⊙O相切于点 ![]() ,
,
∴ ![]() ,
,
∴![]() .
.
∴ ![]() 是等腰直角三角形,
是等腰直角三角形,
∴ ![]()
(2)解:由第(1)问可知 ![]() 是等腰直角三角形,∴
是等腰直角三角形,∴ ![]() ,
,
∴ ![]() ,
,
由勾股定理得 ![]()
![]()
![]() ,
,
∴ ![]()
【解析】(1)根据同弧所对的圆周角等于圆心角的一半得出∠ C O D = 2 ∠ A ,又因∠ D = 2 ∠ A ,从而得出∠ C O D = ∠ D ;根据圆的切线垂直于经过切点的半径得出O C ⊥ P D ,故∠ O C D = 90 ° ,从而得出△ O C D 是等腰直角三角形,故∠ D = 45 ° ;
(2)根据由第(1)问可知 △ O C D 是等腰直角三角形及同圆的半径相等得出O C = C D = 2 =OB;根据勾股定理得出OD的长度,再根据线段的和差得出BD的长度。


科目:初中数学 来源: 题型:
【题目】 解下列各题
(1)解方程x+![]() ;
;
(2)在解方程练习时,学习卷中有一个方程“2y﹣![]() =
=![]() y+■”中的■没印清,小聪问老师,老师只是说:“■是一个有理数,该方程的解与当x=2时,代数式5(x﹣1)﹣2(x﹣2)﹣4的值相同,”小聪很快补上了这个常数,同学们,你们能补上这个常数吗?
y+■”中的■没印清,小聪问老师,老师只是说:“■是一个有理数,该方程的解与当x=2时,代数式5(x﹣1)﹣2(x﹣2)﹣4的值相同,”小聪很快补上了这个常数,同学们,你们能补上这个常数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人是NBA联盟凯尔特人队的两位明星球员,两人在前五个赛季的罚球
命中率如下表所示:
甲球员的命中率(%) | 87 | 86 | 83 | 85 | 79 |
乙球员的命中率(%) | 87 | 85 | 84 | 80 | 84 |
(1)分别求出甲,乙两位球员在前五个赛季罚球的平均命中率;
(2)在某场比赛中,因对方球员技术犯规需要凯尔特人队选派一名队员进行罚球,你认为甲,乙两位球员谁来罚球更好?(请通过计算说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角∠α的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,抛物线y=x2-+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).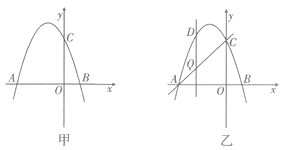
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ![]() ,求点P的坐标;
,求点P的坐标;
(3)如图乙,设点Q是线段AC上的一动点,作DQ ![]() x轴,交抛物线于点D,求线段DQ长度的最大值.
x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在城镇化建设中,开发商要处理A地大量的建筑垃圾,A地只能容纳1台装卸机作业,装卸机平均每6分钟可以给工程车装满一车建筑垃圾,每辆工程车要将建筑垃圾运送至20千米的B处倾倒,每次倾倒时间约为1分钟,倾倒后立即返回A地等候下一次装运,直到装运完毕;工程车的平均速度为40千米/时.
(1)一辆工程车运送一趟建筑垃圾(从装车到返回)需要多少分钟?
(2)至少安排多少辆工程车既能保证装卸机不空闲,又能保证工程车最少等候时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com