
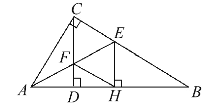
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() 于
于![]() .连接
.连接![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.
【答案】详见解析
【解析】
求出CE=EH,AC=AH,证△CAF≌△HAF,推出∠ACD=∠AHF,求出∠B=∠ACD=∠FHA,推出HF∥CE,推出CF∥EH,得出平行四边形CFHE,根据菱形判定推出即可.
∵∠ACB=90°,AE平分∠BAC,EH⊥AB,
∴CE=EH,
在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,
∴Rt△ACE≌ Rt△AHE(HL),
∴AC=AH,
∵AE平分∠CAB,
∴∠CAF=∠HAF,
在△CAF和△HAF中,
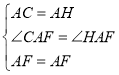 ,
,
∴△CAF≌△HAF(SAS),
∴∠ACD=∠AHF,
∵CD⊥AB,∠ACB=90°,
∴∠CDA=∠ACB=90°,
∴∠B+∠CAB=90°,∠CAB+∠ACD=90°,
∴∠ACD=∠B=∠AHF,
∴FH∥CE,
∵CD⊥AB,EH⊥AB,
∴CF∥EH,
∴四边形CFHE是平行四边形,
∵CE=EH,
∴四边形CFHE是菱形.


科目:初中数学 来源: 题型:
【题目】如图,点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点,且HG与EF交于点I,连接HE、FG,若AB=6,BC=5,EF//AD,HG//AB,则HE+FG的最小值是_____ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距50千米,某日下午甲、乙两人分别骑自行车和骑摩托车从A地出发驶往B地如图所示,图中的折线PQR和线段MN分别表示甲、乙两人所行驶的路程S(千米)与该日下午时间t(时)之间的关系.请根据图象解答下列问题:
(1)直接写出:甲骑自行车出发 小时后,乙骑摩托车才开始出发;乙骑摩托车比甲骑自行车提前 小时先到达B地;
(2)求出乙骑摩托车的行驶速度;甲骑自行车在下午2时至5时的行驶速度;
(3)当甲、乙两人途中相遇时,直接写出相遇地与A地的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
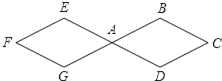
A. 点F B. 点E C. 点A D. 点C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |

请你结合图表中所提供的信息,回答下列问题:
(1)表中m= ,n= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,![]() 这一组所占圆心角的度数为 度;
这一组所占圆心角的度数为 度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com