
【题目】如图甲,抛物线y=x2-+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).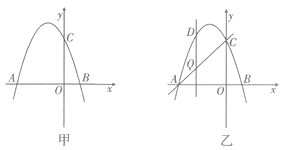
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ![]() ,求点P的坐标;
,求点P的坐标;
(3)如图乙,设点Q是线段AC上的一动点,作DQ ![]() x轴,交抛物线于点D,求线段DQ长度的最大值.
x轴,交抛物线于点D,求线段DQ长度的最大值.
【答案】
(1)解:把A(3,0),C(0,3)代入y=x2+bx+c ,
得 ![]() 解得
解得 ![]()
故该抛物线的解析式为:y=x22x+3 .
(2)解:设 ;P(x,x22x+3) ,由(1)知,该抛物线的解析式为y=x22x+3,则B(1,0).
∵S△AOP=4S△BOC ,
∴ ![]() ×3×|x22x+3|=4×
×3×|x22x+3|=4× ![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x7=0,
解得x=1或x=1± ![]() .
.
则符合条件的点P的坐标为:(1,4)或(1+ ![]() ,4)或(1
,4)或(1 ![]() ,4) 。
,4) 。
(3)解:设直线AC的解析式为y=kx+t , 将A(3,0),C(0,3)代入,
得 ![]() 解得
解得 ![]()
即直线AC的解析式为y=x+3.
设Q点坐标为(x , x+3)(3≤x≤0),则D点坐标为(x , x22x+3),
QD=(x22x+3)(x+3)=x23x= ![]() +
+ ![]() ,
,
∴当x= ![]() 时,QD有最大值
时,QD有最大值 ![]() 。
。
【解析】(1)用待定系数法求出抛物线的解析式;
(2)设出P点的坐标,P(x,x22x+3) ,根据平抛物线的解析式求出其与x轴的另一个交点B的坐标,然后根据三角形的面积公式及S△AOP=4S△BOC , 列出关于x的一元二次方程![]() ×3×|x22x+3|=4×
×3×|x22x+3|=4× ![]() ×1×3;整理得到(x+1)2=0或x2+2x7=0,求解得出x的值,从而得出符合条件的点P的坐标;
×1×3;整理得到(x+1)2=0或x2+2x7=0,求解得出x的值,从而得出符合条件的点P的坐标;
(3)先用待定系数法求出直线AC的解析式,然后设出Q点坐标为(x , x+3)(3≤x≤0),则D点坐标为(x , x2![]() ) 2 +
) 2 + ![]() ,从而得出答案。
,从而得出答案。


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数y= ![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1) 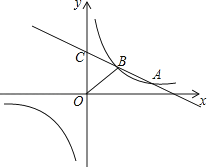
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距50千米,某日下午甲、乙两人分别骑自行车和骑摩托车从A地出发驶往B地如图所示,图中的折线PQR和线段MN分别表示甲、乙两人所行驶的路程S(千米)与该日下午时间t(时)之间的关系.请根据图象解答下列问题:
(1)直接写出:甲骑自行车出发 小时后,乙骑摩托车才开始出发;乙骑摩托车比甲骑自行车提前 小时先到达B地;
(2)求出乙骑摩托车的行驶速度;甲骑自行车在下午2时至5时的行驶速度;
(3)当甲、乙两人途中相遇时,直接写出相遇地与A地的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |

请你结合图表中所提供的信息,回答下列问题:
(1)表中m= ,n= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,![]() 这一组所占圆心角的度数为 度;
这一组所占圆心角的度数为 度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,E是BC延长线上一点,AE交CD于点G,F是AE上一点,并且AC=CF=EF,∠AEB=15°.
(1)求∠ACF的度数;
(2)证明:矩形ABCD为正方形.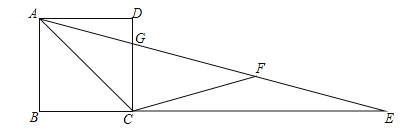
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com