
【题目】如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
A.![]()
B.2![]()
C.![]()
D.1
【答案】A
【解析】解:连接AE,OD、OE.
∵AB是直径,
∴∠AEB=90°,
又∵∠BED=120°,
∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD
∴△AOD是等边三角形,
∴∠OAD=60°,
∵点E为BC的中点,∠AEB=90°,
∴AB=AC,
∴△ABC是等边三角形,边长是4.△EDC是等边三角形,边长是2.
∴∠BOE=∠EOD=60°,
∴![]() 和弦BE围成的部分的面积=
和弦BE围成的部分的面积=![]() 和弦DE围成的部分的面积.
和弦DE围成的部分的面积.
∴阴影部分的面积=S△EDC=![]() ×22=
×22=![]() .
.
故选:A.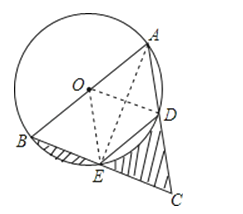
首先证明△ABC是等边三角形.则△EDC是等边三角形,边长是2.而![]() 和弦BE围成的部分的面积=
和弦BE围成的部分的面积=![]() 和弦DE围成的部分的面积.据此即可求解.
和弦DE围成的部分的面积.据此即可求解.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC的中心,射线OE交AB边于点E,OF交BC边于点F,若△ABC的面积为S,∠EOF=120°,则当∠EOF绕点O旋转时,得到的阴影面积发生变化吗?下面有三名同学提出了各自的观点.
甲:阴影部分的面积会发生变化,且当OE,OF分别与△ABC的边垂直时,阴影部分的面积最小.
乙:阴影部分的面积会发生变化,且当E,F分别与△ABC的顶点重合时,阴影部分的面积最大.
丙:无论怎样旋转,阴影部分的面积都保持不变.
你支持谁的观点?____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角∠α的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,抛物线y=x2-+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).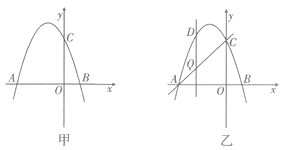
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ![]() ,求点P的坐标;
,求点P的坐标;
(3)如图乙,设点Q是线段AC上的一动点,作DQ ![]() x轴,交抛物线于点D,求线段DQ长度的最大值.
x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面证明:

(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b.
证明:∵a⊥c (已知)
∴∠1= (垂直定义)
∵b∥c (已知)
∴∠1=∠2 ( )
∴∠2=∠1=90° ( )
∴a⊥b ( )
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE.
证明:∵AB∥CD (已知)
∴∠B= ( )
∵∠B+∠D=180° (已知)
∴∠C+∠D=180° ( )
∴CB∥DE ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在城镇化建设中,开发商要处理A地大量的建筑垃圾,A地只能容纳1台装卸机作业,装卸机平均每6分钟可以给工程车装满一车建筑垃圾,每辆工程车要将建筑垃圾运送至20千米的B处倾倒,每次倾倒时间约为1分钟,倾倒后立即返回A地等候下一次装运,直到装运完毕;工程车的平均速度为40千米/时.
(1)一辆工程车运送一趟建筑垃圾(从装车到返回)需要多少分钟?
(2)至少安排多少辆工程车既能保证装卸机不空闲,又能保证工程车最少等候时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:用“十字相乘法”分解因式2x2﹣x﹣3的方法.
(i)二次项系数2=1×2;
(ii)常数项﹣3=﹣1×3=1×(﹣3),验算:“交叉相乘之和”;
1×3+2×(﹣1)=1 1×(﹣1)+2×3=5 1×(﹣3)+2×1=﹣1 1×1+2×(﹣3)=﹣5
(iii)发现第③个“交叉相乘之和”的结果1×(﹣3)+2×1=﹣1,等于一次项系数﹣1.
即:(x+1)(2x﹣3)=2x2﹣3x+2x﹣3=2x2﹣x﹣3,则2x2﹣x﹣3=(x+1)(2x﹣3).
像这样,通过十字交叉线帮助,把二次三项式分解因式的方法,叫做十字相乘法.仿照以上方法,分解因式:3x2+5x﹣12= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0.
(1)当t=3时,解这个方程;
(2)若m,n是方程的两个实数根,设Q=(m﹣2)(n﹣2),试求Q的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com