
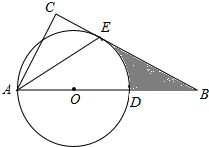
 如图,在△ABC中,AE是它的角平分线,∠C=90°,∠B=30°,D在AB边上,AD=4,以AD为直径的圆O经过点E.
如图,在△ABC中,AE是它的角平分线,∠C=90°,∠B=30°,D在AB边上,AD=4,以AD为直径的圆O经过点E.分析 (1)直接利用角平分线的性质结合等腰三角形的性质得出∠CAE=∠OEA,进而得出∠OEB=90°,即可得出答案;
(2)首先求出EO,BE的长,进而利用阴影部分的面积=S△EOB-S扇形EOD,进而得出答案.
解答 (1)证明:连接OE,
∵AE平分∠CAB,
∴∠CAE=∠EAB,
∵AO=EO,
∴∠OAE=∠AEO,
∴∠CAE=∠OEA,
∴AC∥EO,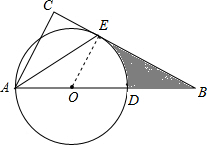
∵∠C=90°,
∴∠OEB=90°,
∴BC是⊙O的切线;
(2)解:∵∠B=30°,∠OEB=90°,
∴EO=$\frac{1}{2}$BO,∠EOB=60°,
∵AD=4,
∴EO=2,DO=2,
∴BO=4,
∴BE=2$\sqrt{3}$,
图中阴影部分的面积为:$\frac{1}{2}$×EO×BE-$\frac{60π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π.
点评 此题主要考查了切线的判定与性质以及扇形面积求法,正确得出BE的长是解题关键.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
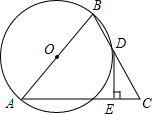 已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.
已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,E是BC上一点,连接AE,作BF⊥AE,垂足为点H,交CD于点F.作CG∥AE,交BF于点G.
如图,在正方形ABCD中,E是BC上一点,连接AE,作BF⊥AE,垂足为点H,交CD于点F.作CG∥AE,交BF于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
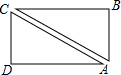 传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?
传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com