
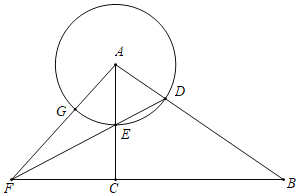
【题目】在Rt△ABC中,∠ACB=90°,AC=15,sin∠BAC=![]() .点D在边AB上(不与点A、B重合),以AD为半径的⊙A与射线AC相交于点E,射线DE与射线BC相交于点F,射线AF与⊙A交于点G.
.点D在边AB上(不与点A、B重合),以AD为半径的⊙A与射线AC相交于点E,射线DE与射线BC相交于点F,射线AF与⊙A交于点G.
(1)如图,设AD=x,用x的代数式表示DE的长;
(2)如果点E是![]() 的中点,求∠DFA的余切值;
的中点,求∠DFA的余切值;
(3)如果△AFD为直角三角形,求DE的长.
【答案】(1)![]() ;(2)∠DFA的余切值为
;(2)∠DFA的余切值为![]() ;(3)DE的长为
;(3)DE的长为![]() 或
或![]() .
.
【解析】
(1)过点D作DH⊥AC,垂足为H.根据锐角三角函数和勾股定理即可用x的代数式表示DE的长;
(2)根据题意可设BC=4k(k>0),AB=5k,则AC=![]() =3k.过点A作AM⊥DE,垂足为M,再根据锐角三角函数和勾股定理即可表示∠DFA的余切值;
=3k.过点A作AM⊥DE,垂足为M,再根据锐角三角函数和勾股定理即可表示∠DFA的余切值;
(3)分两种情况讨论:当点E在AC上时,只有可能∠FAD=90°;当点E在AC的延长线上时,只有可能∠AFD=90°,此时∠AFC=∠AEF.根据锐角三角函数和勾股定理即可求DE的长.
解:(1)如图,
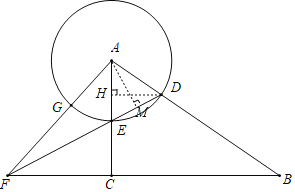
过点D作DH⊥AC,垂足为H.
在Rt△AEH中,![]() ,
,
![]() .
.
在⊙A中,AE=AD=x,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴可设BC=4k(k>0),AB=5k,
则AC=![]() =3k.
=3k.
∵AC=15,
∴3k=15,
∴k=5.
∴BC=20,AB=25.
∵点E是![]() 的中点,由题意可知此时点E在边AC上,点F在BC的延长线上,
的中点,由题意可知此时点E在边AC上,点F在BC的延长线上,
∴∠FAC=∠BAC.
∵∠FCA=∠BCA=90°,AC=AC,
∴△FCA≌△BCA(ASA),
∴FC=BC=20.
∵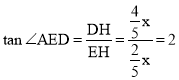 ,
,
又∵∠AED=∠FEC,且∠AED、∠FEC都为锐角,
∴tan∠FEC=2.
∴![]() .
.
∴AE=AC﹣EC=15﹣10=5.
过点A作AM⊥DE,垂足为M,
则![]() .
.
∵ ,
,
∴![]() .
.
在Rt△EFC中,![]() .
.
∴在Rt△AFM中,![]() .
.
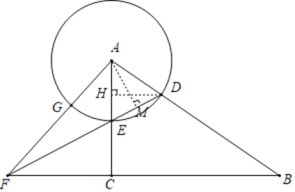
答:∠DFA的余切值为![]() ;
;
(3)当点E在AC上时,只有可能∠FAD=90°.
∵FC=CEtan∠FEC=2(15﹣x),
∴![]() .
.
∴![]() .
.
∵![]() ,
,
又∵∠AED=∠ADE,且∠AED、∠ADE都为锐角,
∴![]() .
.
∴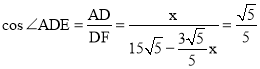 .
.
∴AD=x=![]() .
.
∴![]() .
.
当点E在AC的延长线上时,只有可能∠AFD=90°,
![]()
![]()
![]() ∠AFC=∠AEF.
∠AFC=∠AEF.
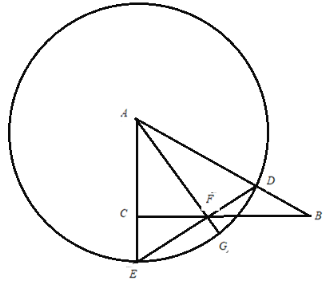
∵∠AFC、∠AEF都为锐角,
∴tan∠AEF=tan∠AFC=2.
∵CE=AE﹣AC=x﹣15,
∴CF=CEtan∠AEF=2(x﹣15).
∴![]() .
.
∴AD=x=![]() .
.
∴.
综上所述,△AFD为直角三角形时,DE的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.选凉亭A,C作为观测点.如图,现测得∠CAB=45°,∠ACB=98°,AC=200米,请计算A,B两个凉亭之间的距离、(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑”是中考体育考试项目之一.某中学为了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑的时间的长短依次分为A,B,C,D四个等级进行统计,并绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
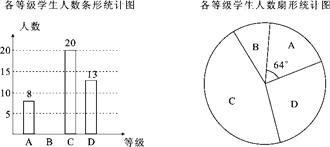
(1)在这次调查中共抽取了 名学生,扇形统计图中,D类所对应的扇形圆心角大小为 ;
(2)所抽取学生“长跑”测试成绩的中位数会落在 等级;
(3)若该校九年级共有900名学生,请你估计该校C等级的学生约在多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
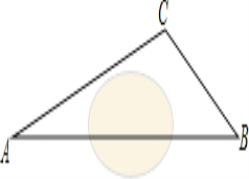
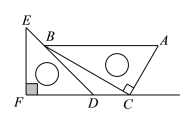
【题目】将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,∠F=∠ACB=90°,AB∥CF,∠E=45°,∠A=60°,AC=8,则CD的长度是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把一个四边形分成两部分,这两部分图形的周长相等,那么这条直线称为这个四边形的“等分周长线”.在直角梯形ABCD中,AB∥CD,∠A=90°,DC=AD,∠B是锐角,cotB=![]() ,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在疫情防控期间,某中学为保障广大师生生命健康安全购进一批免洗手消毒液和84消毒液.如果购买100瓶免洗手消毒液和150瓶84消毒液,共需花费1500元;如果购买120瓶免洗手消毒液和160瓶84消毒液,共需花费1720元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)某药店出售免洗手消毒液,满150瓶免费赠送10瓶84消毒液.若学校从该药店购进免洗手消毒液和84消毒液共230瓶,恰好用去1700元,则学校购买免洗手消毒液多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
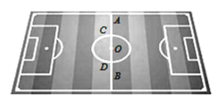
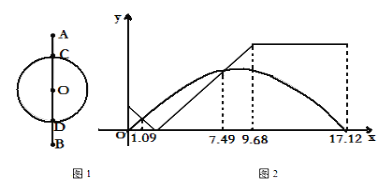
【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC=DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的有________.(填序号)
①小红的运动路程比小兰的长;② 两人分别在1.09秒和7.49秒的时刻相遇;③ 当小红运动到点D的时候,小兰已经经过了点D ;④在4.84秒时,两人的距离正好等于⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
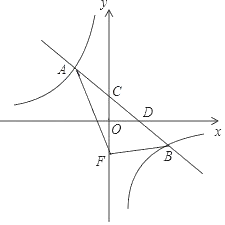
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com