
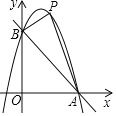
【题目】如图,抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0).
(1)求抛物线的函数表达式和直线的函数表达式;
(2)若点P是抛物线落在第一象限,连接PA,PB,求△PAB的面积S的最大值及此时点P的坐标.
【答案】(1)y=-x2+2x+3;y=-x+3(2)当a=![]() 时,S△PAB有最大值,最大值为
时,S△PAB有最大值,最大值为![]() ,此时点P坐标为(
,此时点P坐标为(![]() ,
,![]() )
)
【解析】
(1)由A、B的坐标,利用待定系数法即可求得函数解析式;
(2)过P点作PN⊥OA于N,交直线B于M,设点P横坐标为a,则可分别表示出P、M的纵坐标,从而表示出PM的长,根据S△PAB=S△PAM+S△PBM得到S=![]() PMOA=-
PMOA=-![]() (a-
(a-![]() )2+
)2+![]() ,利用二次函数的性质可求得其最大值,及此时的点P的坐标.
,利用二次函数的性质可求得其最大值,及此时的点P的坐标.
(1)∵抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的函数表达式是y=-x2+2x+3;
设直线AB:y=kx+m,
根据题意得![]() ,解得
,解得![]() ,
,
∴直线AB的函数表达式是y=-x+3;
(2)如图,过P点作PN⊥OA于N,交直线B于M,设点P横坐标为a,则点P的坐标为(a,-a2+2a+3),点M的坐标是(a,-a+3),

又点P,M在第一象限,
∴PM=-a2+2a+3-(-a+3)=-a2+3a,
∴S△PAB=S△PAM+S△PBM=![]() PMOA=
PMOA=![]() (-a2+3a)×3=-
(-a2+3a)×3=-![]() (a-
(a-![]() )2+
)2+![]() ,
,
∴当a=![]() 时,S△PAB有最大值,最大值为
时,S△PAB有最大值,最大值为![]() ,
,
此时点P坐标为(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ABD=60°,那么∠BAE的度数是( )

A. 40°B. 55°C. 75°D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
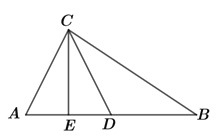
【题目】如图所示.在Rt△ABC中,CD是斜边上的中线,CE是高.已知AB=10cm,DE=2.5cm,则∠BDC=____________度,S△BCD=______cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,5),B(n,2)是抛物线C1:![]() 上的两点,将抛物线C1向左平移,得到抛物线C2,点A,B的对应点分别为点A',B'.若曲线段AB扫过的阴影部分面积为9,则抛物线C2的解析式是______________________________.
上的两点,将抛物线C1向左平移,得到抛物线C2,点A,B的对应点分别为点A',B'.若曲线段AB扫过的阴影部分面积为9,则抛物线C2的解析式是______________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
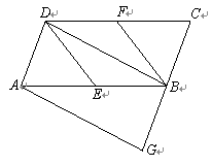
【题目】如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
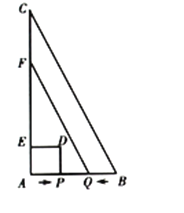
【题目】如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm,动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P, Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为![]() ,正方形APDE和梯形BCFQ重合部分的面积为
,正方形APDE和梯形BCFQ重合部分的面积为![]() cm.
cm.
(1)当![]() =_____s时,点P与点Q重合;
=_____s时,点P与点Q重合;
(2)当![]() 为多少时,点D在QF上;
为多少时,点D在QF上;
(3)是否存在某一时刻,使得正方形APDE的面积被直线QF平分?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
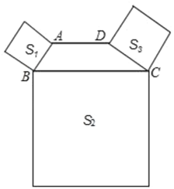
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=2,S3=4,则S2的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com