
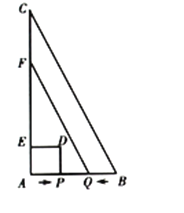
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯA=90ЁуЃЌAB=2cm,AC=4cm,ЖЏЕуPДгЕуAГіЗЂЃЌбиABЗНЯђвд1cm/sЕФЫйЖШЯђЕуBдЫЖЏЃЌЖЏЕуQДгЕуBЭЌЪБГіЗЂЃЌбиBAЗНЯђвд1cm/sЕФЫйЖШЯђЕуAдЫЖЏЃЎЕБЕуPЕНДяЕуBЪБЃЌP, QСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎвдAPЮЊвЛБпЯђЩЯзїе§ЗНаЮAPDEЃЌЙ§ЕуQзїQFЁЮBC,НЛACгкЕуF.ЩшЕуPЕФдЫЖЏЪБМфЮЊ![]() ,е§ЗНаЮAPDEКЭЬнаЮBCFQжиКЯВПЗжЕФУцЛ§ЮЊ
,е§ЗНаЮAPDEКЭЬнаЮBCFQжиКЯВПЗжЕФУцЛ§ЮЊ![]() cmЃЎ
cmЃЎ
ЃЈ1ЃЉЕБ![]() =_____sЪБЃЌЕуPгыЕуQжиКЯЃЛ
=_____sЪБЃЌЕуPгыЕуQжиКЯЃЛ
ЃЈ2ЃЉЕБ![]() ЮЊЖрЩйЪБЃЌЕуDдкQFЩЯЃЛ
ЮЊЖрЩйЪБЃЌЕуDдкQFЩЯЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЕУе§ЗНаЮAPDEЕФУцЛ§БЛжБЯпQFЦНЗжЃПШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ1ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЕБЕуPгыЕуQжиКЯЪБЃЌДЫЪБAPЃНBQЃНtЃЌЧвAPЃЋBQЃНABЃН2ЃЌгЩДЫСавЛдЊвЛДЮЗНГЬЧѓГіtЕФжЕЃЛ
ЃЈ2ЃЉЕБЕуDдкQFЩЯЪБЃЌШчЭМ1ЫљЪОЃЌДЫЪБAPЃНBQЃНtЃЎгЩЯрЫЦШ§НЧаЮБШР§ЯпЖЮЙиЯЕПЩЕУPQЃН![]() tЃЌДгЖјгЩЙиЯЕЪНAPЃЋPQЃЋBQЃНABЃН2ЃЌСавЛдЊвЛДЮЗНГЬЧѓГіtЕФжЕЃЛ
tЃЌДгЖјгЩЙиЯЕЪНAPЃЋPQЃЋBQЃНABЃН2ЃЌСавЛдЊвЛДЮЗНГЬЧѓГіtЕФжЕЃЛ
ЃЈ3ЃЉЕБЕуPдкQЃЌBСНЕужЎМфдЫЖЏЃЈВЛАќРЈQЃЌBСНЕуЃЉЃЌ1ЃМtЁм![]() ЪБЃЌШчД№ЭМ3ЫљЪОЃЌДЫЪБжиКЯВПЗжЮЊЬнаЮPDGQЃЎЯШМЦЫуЬнаЮИїБпГЄЃЌШЛКѓРћгУЬнаЮУцЛ§ЙЋЪНЧѓГіSЃЛгЩЬтвтжЊЃЌЕБ1ЃМtЁм
ЪБЃЌШчД№ЭМ3ЫљЪОЃЌДЫЪБжиКЯВПЗжЮЊЬнаЮPDGQЃЎЯШМЦЫуЬнаЮИїБпГЄЃЌШЛКѓРћгУЬнаЮУцЛ§ЙЋЪНЧѓГіSЃЛгЩЬтвтжЊЃЌЕБ1ЃМtЁм![]() ЪБЃЌе§ЗНаЮAPDEЕФУцЛ§БЛжБЯпQFЦНЗжЃЌСаГіЗНГЬЃЌЧѓГіЪБМфtЃЎ
ЪБЃЌе§ЗНаЮAPDEЕФУцЛ§БЛжБЯпQFЦНЗжЃЌСаГіЗНГЬЃЌЧѓГіЪБМфtЃЎ
НтЃКЃЈ1ЃЉЕБЕуPгыЕуQжиКЯЪБЃЌAPЃНBQЃНtЃЌЧвAPЃЋBQЃНABЃН2ЃЌ
ЁрtЃЋtЃН2ЃЌНтЕУtЃН1sЃЌ
ЙЪД№АИЃК1ЃЎ
ЃЈ2ЃЉЕБЕуDдкQFЩЯЪБЃЌШчЭМ1ЫљЪОЃЌДЫЪБAPЃНBQЃНtЃЎ
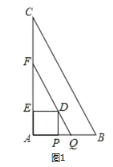
ЁпQFЁЮBCЃЌAPDEЮЊе§ЗНаЮЃЌ
ЁрЁїPQDЁзЁїABCЃЌ
ЁрDPЃКPQЃНACЃКABЃН2ЃЌ
дђPQЃН![]() DPЃН
DPЃН![]() APЃН
APЃН![]() tЃЎ
tЃЎ
гЩAPЃЋPQЃЋBQЃНABЃН2ЃЌЕУtЃЋ![]() tЃЋtЃН2ЃЌ
tЃЋtЃН2ЃЌ
НтЕУЃКtЃН![]() ЃЎ
ЃЎ
ЙЪД№АИЃК![]() ЃЎ
ЃЎ
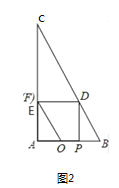
ЃЈ3ЃЉЕБPЁЂQжиКЯЪБЃЌгЩЃЈ1ЃЉжЊЃЌДЫЪБtЃН1ЃЛЕБDЕудкBCЩЯЪБЃЌШчЭМ2ЫљЪОЃЌДЫЪБAPЃНBQЃНtЃЌBPЃН![]() tЃЌЧѓЕУtЃН
tЃЌЧѓЕУtЃН![]() sЃЌвђДЫЕБPЕудкQЃЌBСНЕужЎМфЃЈВЛАќРЈQЃЌBСНЕуЃЉЃЌЧв1ЃМtЁм
sЃЌвђДЫЕБPЕудкQЃЌBСНЕужЎМфЃЈВЛАќРЈQЃЌBСНЕуЃЉЃЌЧв1ЃМtЁм![]() ЪБЃЌШчЭМ3ЫљЪОЃЌДЫЪБжиКЯВПЗжЮЊЬнаЮPDGQЃЎДЫЪБAPЃНBQЃНtЃЌ
ЪБЃЌШчЭМ3ЫљЪОЃЌДЫЪБжиКЯВПЗжЮЊЬнаЮPDGQЃЎДЫЪБAPЃНBQЃНtЃЌ
ЁрAQЃН2tЃЌPQЃНAPAQЃН2t2ЃЛ
взжЊЁїABCЁзЁїAQFЃЌ
ПЩЕУAFЃН2AQЃЌEFЃН2EGЃЎ
ЁрEFЃНAFAEЃН2ЃЈ2tЃЉtЃН43tЃЌEGЃН![]() EFЃН2
EFЃН2![]() tЃЌ
tЃЌ
ЁрDGЃНDEEGЃНtЃЈ2![]() tЃЉЃН
tЃЉЃН![]() t2ЃЎ
t2ЃЎ
SЃНSЬнаЮPDGQЃН![]() ЃЈPQЃЋDGЃЉPDЃЌ
ЃЈPQЃЋDGЃЉPDЃЌ
ЃН![]() [ЃЈ2t2ЃЉЃЋЃЈ
[ЃЈ2t2ЃЉЃЋЃЈ![]() t2ЃЉ]tЃЌ
t2ЃЉ]tЃЌ
ЃН![]() ЃЛ
ЃЛ
гЩЬтвтжЊЃЌЕБ1ЃМtЁм![]() ЪБЃЌе§ЗНаЮAPDEЕФУцЛ§БЛжБЯпQFЦНЗжЃЌ
ЪБЃЌе§ЗНаЮAPDEЕФУцЛ§БЛжБЯпQFЦНЗжЃЌ
Ёр![]()
НтЕУЃК![]()
ЙЪД№АИЮЊЃК![]()


 ФмСІЦРМлЯЕСаД№АИ
ФмСІЦРМлЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
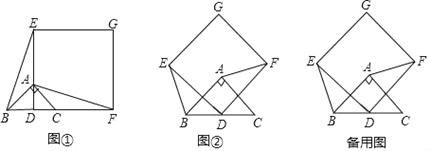
ЁОЬтФПЁП(1)ЮЪЬтЗЂЯжЃКШчЭМЂйЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌЕуDЪЧBCЕФжаЕуЃЌвдЕуDЮЊЖЅЕузїе§ЗНаЮDFGEЃЌЪЙЕуAЁЂCЗжБ№дкDEКЭDFЩЯЃЌСЌНгBEЁЂAFЃЎдђЯпЖЮBEКЭAFЪ§СПЙиЯЕ_____ЃЎ
(2)РрБШЬНОПЃКШчЭМЂкЃЌБЃГжЁїABCЙЬЖЈВЛЖЏЃЌНЋе§ЗНаЮDFGEШЦЕуDа§зЊІС(0ЁуЃМІСЁм360Ёу)ЃЌдђ(1)жаЕФНсТлЪЧЗёГЩСЂЃПШчЙћГЩСЂЃЌЧыжЄУїЃЛШчЙћВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
(3)НтОіЮЪЬтЃКШєBCЃНDFЃН2ЃЌдк(2)ЕФа§зЊЙ§ГЬжаЃЌСЌНгAEЃЌЧыжБНгаДГіAEЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
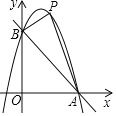
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрНЛгкAЃЌBСНЕуЃЌЧвЕуAЃЈ1ЃЌЃ4ЃЉЮЊХзЮяЯпЕФЖЅЕуЃЌЕуBдкxжсЩЯЁЃ
ЯрНЛгкAЃЌBСНЕуЃЌЧвЕуAЃЈ1ЃЌЃ4ЃЉЮЊХзЮяЯпЕФЖЅЕуЃЌЕуBдкxжсЩЯЁЃ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉжаХзЮяЯпЕФЕкЖўЯѓЯоЭМЯѓЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPOBгыЁїPOCШЋЕШЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуQЪЧyжсЩЯвЛЕуЃЌЧвЁїABQЮЊжБНЧШ§НЧаЮЃЌЧѓЕуQЕФзјБъЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=-x2+bx+cОЙ§ЕуBЃЈ0ЃЌ3ЃЉКЭЕуAЃЈ3ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНКЭжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєЕуPЪЧХзЮяЯпТфдкЕквЛЯѓЯоЃЌСЌНгPAЃЌPBЃЌЧѓЁїPABЕФУцЛ§SЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЁїPBCЁЂЁїQCDЪЧСНИіЕШБпШ§НЧаЮЃЌPBгыDQНЛгкMЃЌBPгыCQНЛгкEЃЌCPгыDQНЛгкFЁЃ
ЧѓжЄЃКPM=QMЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
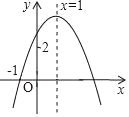
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЕФЖдГЦжсЪЧжБЯпxЃН1ЃЌЧвОЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌдђЯТСаНсТлЃКЂйabcЃМ0ЃЛЂк2aЉbЃН0ЃЛЂлaЃМЉ![]() ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМдкЁїABCжаЃЌADЪЧИпЃЌОиаЮPQMNЕФЖЅЕуPЁЂNЗжБ№дкABЁЂACЩЯЃЌQMдкБпBCЩЯЃЎШєBCЃН8cmЃЌADЃН6cmЃЌ

ЃЈ1ЃЉPNЃН2PQЃЌЧѓОиаЮPQMNЕФжмГЄ
ЃЈ2ЃЉЕБPNЮЊЖрЩйЪБОиаЮPQMNЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
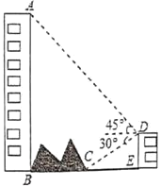
ЁОЬтФПЁПШчЭМЃЌДѓТЅЕзгвВргавЛеЯАЮяЃЌдкеЯАЮяЕФХдБпгавЛДБаЁТЅDEЃЌдкаЁТЅЕФЖЅЖЫDДІВтЕУеЯАЮяБпдЕЕуCЕФИЉНЧЮЊ30ЁуЃЌВтЕУДѓТЅЖЅЖЫAЕФбіНЧЮЊ45ЁуЃЈЕуBЃЌCЃЌEдкЭЌвЛЫЎЦНжБЯпЩЯЃЉ.вбжЊAB=80mЃЌDE=20mЃЌЧѓеЯАЮяBЃЌCСНЕуМфЕФОрРы.ЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮїЙЯОгЊЛЇвд2дЊЃЏЧЇПЫЕФМлИёЙКНјвЛХњаЁаЭЮїЙЯЃЌвд3дЊЃЏЧЇПЫЕФМлИёГіЪлЃЌУПЬьПЩЪлГі200ЧЇПЫЃЌЮЊСЫДйЯњЃЌИУОгЊЛЇОіЖЈНЕМлЯњЪлЃЌОЕїВщЗЂЯжЃЌетжжаЁаЭЮїЙЯУПНЕМл0ЃЎ1дЊЃЏЧЇПЫЃЌУПЬьПЩЖрЪлГі40ЧЇПЫЃЌСэЭтЃЌУПЬьЕФЗПзтЕШЙЬЖЈГЩБОЙВ24дЊЃЎ
(1)ЩшЯњЪлЕЅМлЮЊУПЧЇПЫaдЊ,УПЬьЦНОљЛёРћЮЊyдЊ,ЧыНтД№ЯТСаЮЪЬт:
ЂйУПЬьЦНОљЯњЪлСППЩвдБэЪОЮЊ_____;
ЂкУПЬьЦНОљЯњЪлЖюПЩвдБэЪОЮЊ_____;
ЂлУПЬьЦНОљЛёРћПЩвдБэЪОЮЊy=______;
(2) ИУОгЊЛЇвЊЯыУПЬьгЏРћ200дЊЃЌгІНЋУПЧЇПЫаЁаЭЮїЙЯЕФЪлМлНЕЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com