
【题目】如图在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,

(1)PN=2PQ,求矩形PQMN的周长
(2)当PN为多少时矩形PQMN的面积最大,最大值为多少?
【答案】(1)矩形PQMN的周长=14.4cm;(2)当AE=3时,矩形PQMN的面积最大,最大面积是12,此时PN=4.
【解析】
(1)由题意可得出PQ:AD=BP:AB,PN:BC=AP:AB,BC=8,AD=6,据此可得出PQ,PN的值,故可得出矩形PQMN的周长;
(2)设长方形零件PQMN的边AE=x,矩形PQMN的面积为S,利用△APN∽△ABC得相似比,用相似比可得出用含x的式子表示S,从而得出二次函数解析式,根据解析式及自变量取值范围求S的最大值.
(1)由题意得;PQ:AD=BP:AB,PN:BC=AP:AB
∴![]() ,
,
又∵PN=2PQ,BC=8cm,AD=6cm,
∴![]() ,
,
∴PQ=2.4
则PN=4.8,
∴矩形PQMN的周长=14.4cm;
(2)∵四边形PQMN是矩形,
∴PN∥BC,∠PQM=90°,∠QPN=90°,
∴△PAN∽△ABC,
∵AD是高,
∴∠ADB=90°,
∴四边形PQDE是矩形,∠AEN=90°,
∴![]() ,PQ=DE,
,PQ=DE,
设AE=x,矩形PQMN的面积为S,
则![]() ,DE=6﹣x,
,DE=6﹣x,
∴PN=![]() x,PQ=6﹣x,
x,PQ=6﹣x,
∴S=﹣![]() x2+8x.
x2+8x.
∴当x=![]() =3时,S的最大值为12.,
=3时,S的最大值为12.,
∴当AE=3时,矩形PQMN的面积最大,最大面积是12,此时PN=![]() ×3=4.
×3=4.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
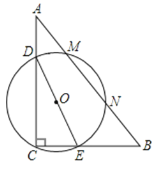
【题目】如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6 ,若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,5),B(n,2)是抛物线C1:![]() 上的两点,将抛物线C1向左平移,得到抛物线C2,点A,B的对应点分别为点A',B'.若曲线段AB扫过的阴影部分面积为9,则抛物线C2的解析式是______________________________.
上的两点,将抛物线C1向左平移,得到抛物线C2,点A,B的对应点分别为点A',B'.若曲线段AB扫过的阴影部分面积为9,则抛物线C2的解析式是______________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
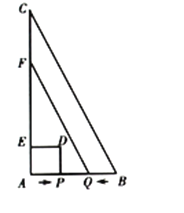
【题目】如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm,动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P, Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为![]() ,正方形APDE和梯形BCFQ重合部分的面积为
,正方形APDE和梯形BCFQ重合部分的面积为![]() cm.
cm.
(1)当![]() =_____s时,点P与点Q重合;
=_____s时,点P与点Q重合;
(2)当![]() 为多少时,点D在QF上;
为多少时,点D在QF上;
(3)是否存在某一时刻,使得正方形APDE的面积被直线QF平分?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
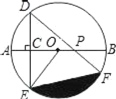
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2![]() ,∠DPA=45°.则图中阴影部分的面积为____.
,∠DPA=45°.则图中阴影部分的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
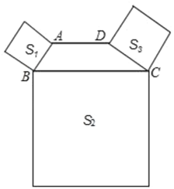
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=2,S3=4,则S2的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
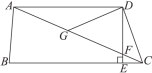
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=1,则DE的长为( )
A. 2![]() B. 4C. 2
B. 4C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
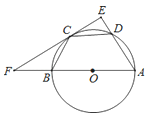
【题目】如图,AB是⊙O的直径,C,D在⊙O上,且BC=CD,过点C作CE⊥AD,交AD延长线于E,交AB延长线于F点.若AB=4ED,则cos∠ABC的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
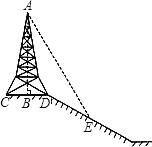
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=20m,DE=30m,小明和小华的身高都是1.5m,同一时刻,小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com