
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЛЮвУЧжЊЕР![]() ЕФМИКЮвтвхЪЧдкЪ§жсЩЯЪ§
ЕФМИКЮвтвхЪЧдкЪ§жсЩЯЪ§![]() ЖдгІЕФЕугыдЕуЕФОрРыЃЌМД
ЖдгІЕФЕугыдЕуЕФОрРыЃЌМД![]() ЃЌвВОЭЪЧЫЕЃЌ
ЃЌвВОЭЪЧЫЕЃЌ![]() БэЪОдкЪ§жсЩЯЪ§
БэЪОдкЪ§жсЩЯЪ§![]() гыЪ§0ЖдгІЕужЎМфЕФОрРыЃЎетИіНсТлПЩвдЭЦЙуЮЊЃК
гыЪ§0ЖдгІЕужЎМфЕФОрРыЃЎетИіНсТлПЩвдЭЦЙуЮЊЃК![]() БэЪОдкЪ§жсЩЯЪ§
БэЪОдкЪ§жсЩЯЪ§![]() гы
гы![]() ЖдгІЕужЎМфЕФОрРыЃЎР§ЃКвбжЊ
ЖдгІЕужЎМфЕФОрРыЃЎР§ЃКвбжЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
НтЃКдкЪ§жсЩЯгы1ЕФОрРыЮЊ2ЕФЕуЖдгІЪ§ЮЊ3КЭ![]() ЃЌМД
ЃЌМД![]() ЕФжЕЮЊ3КЭ
ЕФжЕЮЊ3КЭ![]() ЃЎ
ЃЎ
ЗТеедФЖСВФСЯЕФНтЗЈЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЕФжЕЮЊ__________ЃЛ
ЕФжЕЮЊ__________ЃЛ
ЃЈ2ЃЉШєЪ§жсЩЯБэЪО![]() ЕФЕудк
ЕФЕудк![]() гы2жЎМфЃЌдђ
гы2жЎМфЃЌдђ![]() ЕФжЕЮЊ__________ЃЛ
ЕФжЕЮЊ__________ЃЛ
ЃЈ3ЃЉЕБ![]() ТњзуЪВУДЬѕМўЪБЃЌ
ТњзуЪВУДЬѕМўЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЪЧЖрЩйЃЎ
газюаЁжЕЃЌзюаЁжЕЪЧЖрЩйЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2КЭ-6ЃЛЃЈ2ЃЉ6ЃЛЃЈ3ЃЉ![]() ЪБЃЌгазюаЁжЕ3ЃЎ
ЪБЃЌгазюаЁжЕ3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩдФЖСВФСЯжаЕФЗНЗЈЧѓГіaЕФжЕМДПЩЃЛ
ЃЈ2ЃЉЗНЗЈвЛЃКИљОнaЕФЗЖЮЇХаЖЯГіОјЖджЕРяУцЪНзгЕФе§ИКЃЌРћгУОјЖджЕЕФДњЪ§втвхЛЏМђЃЌКЯВЂМДПЩЕУЕННсЙћЃЛЗНЗЈЖўЃК![]() БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ-4ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ2ЕФЕужЎМфЕФОрРыЕФКЭЃЌЕББэЪО
БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ-4ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ2ЕФЕужЎМфЕФОрРыЕФКЭЃЌЕББэЪО![]() ЕФЕудк
ЕФЕудк![]() гы2жЎМфЪБЃЌ
гы2жЎМфЪБЃЌ![]() ЕШгкБэЪО2гы-4ЕФЕужЎМфЕФОрРыЃЌДгЖјПЩЕУГіНсЙћЃЛ
ЕШгкБэЪО2гы-4ЕФЕужЎМфЕФОрРыЃЌДгЖјПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉЗНЗЈвЛЃКЗжaЃМ-2ЃЌ-2ЁмaЁм1ЃЌaЃО1Ш§жжЧщПіЗжБ№ЛЏМђдЪНЃЌДгЖјПЩЕУГіНсЙћЃЛЗНЗЈЖўЃКгЩ![]() БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ1ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ-2ЕФЕужЎМфЕФОрРыЕФКЭЃЌвЊЧѓЫќЕФзюаЁжЕЃЌПЩЕУГіЕББэЪОaЕФЕудк-2гы1жЎМфЪБШЁЕУзюаЁжЕЃЌДгЖјПЩЕУГіНсЙћЃЎ
БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ1ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ-2ЕФЕужЎМфЕФОрРыЕФКЭЃЌвЊЧѓЫќЕФзюаЁжЕЃЌПЩЕУГіЕББэЪОaЕФЕудк-2гы1жЎМфЪБШЁЕУзюаЁжЕЃЌДгЖјПЩЕУГіНсЙћЃЎ
НтЃКЃЈ1ЃЉдкЪ§жсЩЯгы-2ОрРыЮЊ4ЕФЕуЕФЖдгІЪ§ЮЊ-6КЭ2ЃЌМДaЕФжЕЮЊ-6КЭ2ЃЌ
ЙЪД№АИЮЊЃК-6КЭ2ЃЛ
ЃЈ2ЃЉЗНЗЈвЛЃКИљОнЬтвтЕУЃК-4ЃМaЃМ2ЃЌ
Ёрa+4ЃО0ЃЌa-2ЃМ0ЃЌ
ЁрдЪН=a+4+2-a=6ЃЌ
ЗНЗЈЖўЃКЁп![]() БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ-4ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ2ЕФЕужЎМфЕФОрРыЕФКЭЃЌ
БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ-4ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ2ЕФЕужЎМфЕФОрРыЕФКЭЃЌ
ЁрЕБЪ§жсЩЯБэЪО![]() ЕФЕудк
ЕФЕудк![]() гы2жЎМфЪБЃЌ
гы2жЎМфЪБЃЌ![]() =|2-ЃЈ-4ЃЉ|=6ЃЛ
=|2-ЃЈ-4ЃЉ|=6ЃЛ
ЙЪД№АИЮЊЃК6ЃЛ
ЃЈ3ЃЉЗНЗЈвЛЃКЕБ![]() ЪБЃЌдЪН
ЪБЃЌдЪН![]() ЃО3ЃЛ
ЃО3ЃЛ
ЕБ![]() ЪБЃЌдЪН
ЪБЃЌдЪН![]() ЃЛ
ЃЛ
ЕБaЃО1ЪБЃЌдЪН![]() ЃО3ЃЌ
ЃО3ЃЌ
ЁрЕБ![]() ЪБЃЌдЪНгазюаЁжЕ3ЃЎ
ЪБЃЌдЪНгазюаЁжЕ3ЃЎ
ЗНЗЈЖўЃКЁп![]() БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ1ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ-2ЕФЕужЎМфЕФОрРыЕФКЭЃЌ
БэЪОдкЪ§жсЩЯБэЪОЪ§aЃЌ1ЕФЕужЎМфЕФОрРыгыБэЪОaЃЌ-2ЕФЕужЎМфЕФОрРыЕФКЭЃЌ
ЁрЕБЪ§жсЩЯБэЪО![]() ЕФЕудк-2гы1жЎМфЪБЃЌ
ЕФЕудк-2гы1жЎМфЪБЃЌ![]() ШЁЕУзюаЁжЕЃЌ
ШЁЕУзюаЁжЕЃЌ
МДЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕ=|1-ЃЈ-2ЃЉ|=3ЃЎ
газюаЁжЕЃЌзюаЁжЕ=|1-ЃЈ-2ЃЉ|=3ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжНЁЩэЧђЃЌвбжЊетжжНЁЩэЧђЕФГЩБОМлЮЊУПИі20дЊЃЌЪаГЁЕїВщЗЂЯжЃЌИУжжНЁЩэЧђУПЬьЕФЯњЪлСПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉгаШчЯТЙиЯЕЃКy=Љ20x+80ЃЈ20ЁмxЁм40ЃЉЃЌЩшетжжНЁЩэЧђУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
ЃЈ1ЃЉЧѓwгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИУжжНЁЩэЧђЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉШчЙћЮяМлВПУХЙцЖЈетжжНЁЩэЧђЕФЯњЪлЕЅМлВЛИпгк28дЊЃЌИУЩЬЕъЯњЪлетжжНЁЩэЧђУПЬьвЊЛёЕУ150дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
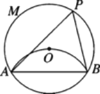
ЁОЬтФПЁПШчЭМЃЌдкдВЁбOжаЃЌНЋЛЁABбиЯвABелЕўЃЌЪЙЛЁABЧЁКУОЙ§дВаФOЃЌЕуPЪЧгХЛЁAMBЩЯвЛЕуЃЌдђЁЯAPBЕФЖШЪ§ЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
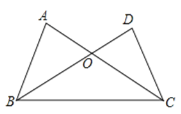
ЁОЬтФПЁПШчЭМЃЌЯТСаЬѕМўжаЃЌВЛФмжЄУїЁїABC Ёе ЁїDCBЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуBЁЂEЁЂCЁЂFдквЛЬѕжБЯпЩЯЃЌACЁЮDEЃЌBE=FCЃЌЁЯA=ЁЯDЃЌ
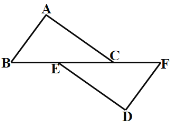
(1) ЧѓжЄЃКAB=DFЃЛ(2)ЧѓжЄЃКABЁЮDFЃЛ(3)ШєBC=9,EC=5ЃЌЧѓBFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
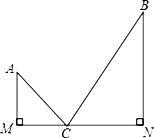
ЁОЬтФПЁПШчЭМЃКжЊЃКAMЁЭMNЃЌBNЁЭMNЃЌДЙзуЗжБ№ЮЊMЃЌNЃЌЕуCЪЧMNЩЯЪЙAC+BCЕФжЕзюаЁЕФЕуЃЎШєAM=3ЃЌBN=5ЃЌMN=15ЃЌдђAC+BC=______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌABЁЭBCЃЌBEЁЭACЃЌЁЯ1=ЁЯ2ЃЌAD=ABЃЌдђЯТСаНсТлВЛе§ШЗЕФЪЧ
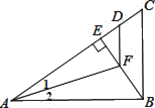
A. BF=DF B. ЁЯ1=ЁЯEFD C. BF>EF D. FDЁЮBC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌDEЃЌDFЗжБ№ЪЧЁїABDКЭЁїACDЕФИпЃЌСЌНгEFНЛADгкG.ЯТСаНсТлЃКЂйADДЙжБЦНЗжEFЃЛЂкEFДЙжБЦНЗжADЃЛЂлADЦНЗжЁЯEDFЃЛЂмЕБЁЯBACЮЊ60ЁуЪБЃЌAG=3DGЃЌЦфжаВЛе§ШЗЕФНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
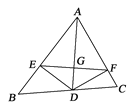
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЕааШЅФъAаЭГЕЕФЯњЪлзмЖюЮЊ6ЭђдЊЃЌНёФъУПСОГЕЕФЪлМлБШШЅФъМѕЩй400дЊЃЎШєТєГіЕФЪ§СПЯрЭЌЃЌЯњЪлзмЖюНЋБШШЅФъМѕЩй20%ЃЎ
ЃЈ1ЃЉЧѓНёФъAаЭГЕУПСОГЕЕФЪлМлЃЎ
ЃЈ2ЃЉИУГЕааМЦЛЎаТНјвЛХњAаЭГЕКЭBаЭГЕЙВ45СОЃЌвбжЊAЁЂBаЭГЕЕФНјЛѕМлИёЗжБ№ЪЧ1100дЊЃЌ1400дЊЃЌНёФъBаЭГЕЕФЯњЪлМлИёЪЧ2000дЊЃЌвЊЧѓBаЭГЕЕФНјЛѕЪ§СПВЛГЌЙ§AаЭГЕЪ§СПЕФСНБЖЃЌгІШчКЮНјЛѕВХФмЪЙетХњГЕЛёЕУзюДѓРћШѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com