
【题目】如图,已知点B、E、C、F在一条直线上,AC∥DE,BE=FC,∠A=∠D,
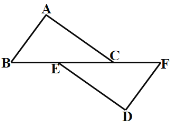
(1) 求证:AB=DF;(2)求证:AB∥DF;(3)若BC=9,EC=5,求BF的长.
【答案】(1)详见解析;(2)详见解析;(3)13.
【解析】
(1)由条件证明△ABC≌△DFE即可求得AB=DF;
(2)由(1)可知,∠ABC=∠DFE,即可判定平行.
(3)由全等三角形的性质可得BC=FE,再利用线段的长和差可求得BF.
证明:(1)∵AC∥DE
∴∠ACB=∠DEF
∵BE=FC
∴BE+EC=FC+EC
∴BC=FE
在△ABC和△DFE中,
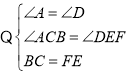
∴△ABC≌△DFE(AAS)
∴![]() AB=DF
AB=DF
(2)由(1)可知,△ABC≌△DFE
∴∠ABC=∠DFE
∴AB∥DF
(3) 由(1)可知,△ABC≌△DFE
∴BC=FE
又∵BC=9,EC=5
∴CF=EF-EC=4
∴BF=BC+CF=9+4=13.
答:BF的长为13.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BD=CE
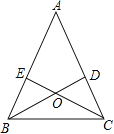
(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:
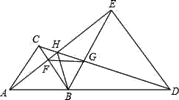
①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤FG∥AD.其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(-36.35)+(-7.25)+26.35+(+7![]() )
)
(3)(﹣99)﹣(+61)﹣(﹣52)+(﹣32)
(4) 49![]() +(-78.21)+27
+(-78.21)+27![]() +(-21.79)
+(-21.79)
(5)![]()
(6)![]()
(7)![]()
(8)![]()
(9) ![]()
(10)![]()
(11) ![]()
(12)![]()
(13)![]() (计算不简便不得分)
(计算不简便不得分)
(14)| —1![]() +(—2
+(—2![]() )| +(—1
)| +(—1![]() )
)
(15)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料;我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数0对应点之间的距离.这个结论可以推广为:
与数0对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.例:已知
对应点之间的距离.例:已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与1的距离为2的点对应数为3和![]() ,即
,即![]() 的值为3和
的值为3和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,
,![]() 的值为__________;
的值为__________;
(2)若数轴上表示![]() 的点在
的点在![]() 与2之间,则
与2之间,则![]() 的值为__________;
的值为__________;
(3)当![]() 满足什么条件时,
满足什么条件时,![]() 有最小值,最小值是多少.
有最小值,最小值是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的课外阅读情况,对部分学生进行了调查,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制如下两幅不完整的统计图.
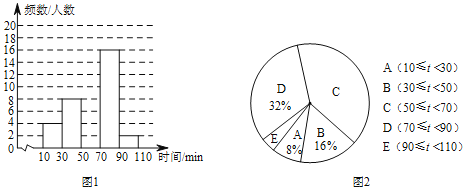
请你根据以上信息解答下列问题:
(1)本次调查活动采取了 调查方式,样本容量是 .
(2)图2中C的圆心角度数为 度,补全图1的频数分布直方图.
(3)该校有900名学生,估计该校学生平均每天的课外阅读时间不少于50min的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com