
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BD=CE
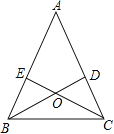
(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
【答案】(1)是,理由参见解析;(2)在,理由参见解析.
【解析】
(1)利用HL证明Rt△BCE≌Rt△DCB,由全等得到∠ABC=∠ACB,从而得到AB=AC,可知△ABC为等腰三角形;
(2)由Rt△BCE≌Rt△DCB,得到BE=CD,再利用AAS证明△EOB≌△DOC,从而得到OE=OD,又因为BD、CE分别是AC、AB上的高,所以OE⊥AB,OD⊥AC,根据角平分线的判定定理可知点O在∠A的平分线上.
(1)![]() BD、CE分别是AC、AB上的高,
BD、CE分别是AC、AB上的高,
![]() ∠CEB=∠BDC=90°
∠CEB=∠BDC=90°
又![]() BD=CE,BC=CB,
BD=CE,BC=CB,
![]() Rt△BCE≌Rt△DCB(HL),
Rt△BCE≌Rt△DCB(HL),
![]() ∠ABC=∠ACB(全等三角形对应角相等)
∠ABC=∠ACB(全等三角形对应角相等)
![]() AB=AC(等角对等边),
AB=AC(等角对等边),
![]() △ABC为等腰三角形;
△ABC为等腰三角形;
(2)![]() Rt△BCE≌Rt△DCB,
Rt△BCE≌Rt△DCB,
![]() BE=CD(全等三角形对应边相等),
BE=CD(全等三角形对应边相等),
在△EOB和△DOC中,∠EOB=∠DOC,∠OEB=∠ODC=90°,
![]() △EOB≌△DOC(AAS),
△EOB≌△DOC(AAS),
![]() OE=OD,
OE=OD,
![]() OE⊥AB,OD⊥AC,根据角平分线的判定定理(到角的两边距离相等的点在这个角的平分线上)可知点O在∠A的平分线上.
OE⊥AB,OD⊥AC,根据角平分线的判定定理(到角的两边距离相等的点在这个角的平分线上)可知点O在∠A的平分线上.


科目:初中数学 来源: 题型:
【题目】如图,AB=20cm,点P从点A出发,沿AB以2cm/s的速度匀速向终点B运动;同时点Q从点B出发,沿BA以4cm/s的速度匀速向终点A运动,设运动时间为ts
(1)填空:PA= cm;BQ= cm;(用含t的代数式表示)
(2)当P、Q两点相遇时,求t的值;
(3)探究:当PQ两点相距5cm时,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为( )
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
查看答案和解析>>
科目:初中数学 来源: 题型:
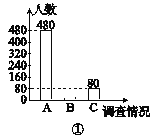
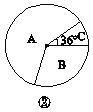
【题目】为了了解初中生毕业后就读普通高中或就读中等职业技术学校的意向,某校对八、九年级部分学生进行了一次调查,调查结果有三种情况:A.只愿意就读普通高中;B.只愿意就读中等职业技术学校;C.就读普通高中或中等职业技术学校都愿意.学校教务处将调查数据进行了整理,并绘制了如图25-3-3所示的尚不完整的统计图,请根据相关信息,解答下列问题:
(1)本次活动共调查了多少名学生?
(2)补全图①,并求出图②中B区域的圆心角的度数;
(3)若该校八、九年级的学生共有2800名,请估计该校八、九年级学生中只愿意就读中等职业技术学校的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为![]() .若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
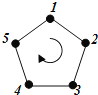
如:小宇同学从编号为![]() 的顶点开始,他应走
的顶点开始,他应走![]() 个边长,即从
个边长,即从![]() 为第一次“移位”,这时他到达编号为
为第一次“移位”,这时他到达编号为![]() 的顶点;然后从
的顶点;然后从![]() 为第二次“移位”,....若小宇同学从编号为
为第二次“移位”,....若小宇同学从编号为![]() 的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AC∥DE,BE=FC,∠A=∠D,
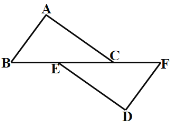
(1) 求证:AB=DF;(2)求证:AB∥DF;(3)若BC=9,EC=5,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com