
【题目】如图,给正五边形的顶点依次编号为![]() .若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
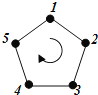
如:小宇同学从编号为![]() 的顶点开始,他应走
的顶点开始,他应走![]() 个边长,即从
个边长,即从![]() 为第一次“移位”,这时他到达编号为
为第一次“移位”,这时他到达编号为![]() 的顶点;然后从
的顶点;然后从![]() 为第二次“移位”,....若小宇同学从编号为
为第二次“移位”,....若小宇同学从编号为![]() 的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点.
(1)如图2,数轴上点A、B表示的数分别为-4、12,点D是线段AB的三等分点,求点D在数轴上所表示的数;
(2)在(1)的条件下,点P从点A出发以每秒1个单位长度的速度在数轴上向右运动;点Q从点B出发,在数轴上先向左运动,与点P重合后立刻改变方向与点P同向而行,且速度始终为每秒3个单位长度,点P、Q同时出发,设运动时间为t秒.
①用含t的式子表示线段AQ的长度;
②当点P是线段AQ的三等分点时,求点P在数轴上所表示的数.
![]()
图1

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BD=CE
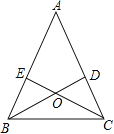
(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东行驶了![]() 千米到达小彬家,继续向东行驶了
千米到达小彬家,继续向东行驶了![]() 千米到达小颖家,然后向西行驶了
千米到达小颖家,然后向西行驶了![]() 千米到达小明家,最后回到超市.
千米到达小明家,最后回到超市.
(1)以超市为原点,向东为正,以![]() 个单位长度表示
个单位长度表示![]() ,在数轴上表示出上述各地点的位置.
,在数轴上表示出上述各地点的位置.
(2)请列式计算小明家在超市什么方向?距超市多远?
(3)若货车每千米油耗![]() 升,这辆货车共耗油多少升?
升,这辆货车共耗油多少升?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公共汽车行驶在笔直的公路上,这条路上有![]() 四个站点,每相邻两站之间的距离为
四个站点,每相邻两站之间的距离为![]() 千米,从
千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔
站同时发车,相向而行,且以后上行车、下行车每隔![]() 分钟分别在
分钟分别在![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为![]() 千米/小时.
千米/小时.
![]() 第一班上行车到
第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
![]() 第一班上行车与第一班下行车发车后多少小时相距
第一班上行车与第一班下行车发车后多少小时相距![]() 千米?
千米?
![]() 一乘客在
一乘客在![]() 两站之间的
两站之间的![]() 处,刚好遇到上行车,
处,刚好遇到上行车,![]() 千米,他从
千米,他从![]() 处以
处以![]() 千米/小时的速度步行到
千米/小时的速度步行到![]() 站乘下行车前往
站乘下行车前往![]() 站办事.
站办事.

①若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
②若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:
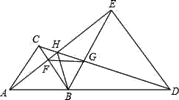
①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤FG∥AD.其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com