
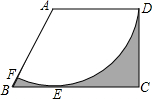
 如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$.
如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$. 分析 连接AE,则AE⊥BC,由AD∥BC,DC⊥BC,易得AE=DC=AD=$\sqrt{3}$,利用锐角三角函数易得∠B=60°,可得∠BAD=120°,可得扇形面积,阴影部分的面积=梯形的面积-扇形的面积,从而求解.
解答 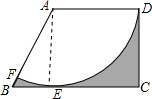 解:连接AE,则AE⊥BC,
解:连接AE,则AE⊥BC,
∵AD∥BC,DC⊥BC,
∴AE=DC=AD=$\sqrt{3}$,
在直角三角形ABE中,tan∠B=$\frac{AE}{BE}$=$\sqrt{3}$,
∴∠B=60°,
∴∠BAE=30°,
∴∠BAD=120°,
∴S扇形DAF=$\frac{120°}{360°}{πR}^{2}$=$\frac{1}{3}×$π×${(\sqrt{3})}^{2}$=π,
S梯形ABCD=$\frac{1}{2}$×(AD+BC)×CD=$\frac{1}{2}×$($\sqrt{3}+\sqrt{3}+1$)×$\sqrt{3}$=3$+\frac{\sqrt{3}}{2}$,
∴S阴影=3$+\frac{\sqrt{3}}{2}$-π.
故答案为:3$+\frac{\sqrt{3}}{2}-π$.
点评 本题主要考查了扇形的面积和梯形的面积计算,利用锐角三角函数得出∠B=60°是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 了解北京市中学生的视力情况 | |
| B. | 调查某品牌食品的色素含量是否符合国家标准 | |
| C. | 了解全班同学参加社会实践活动时间 | |
| D. | 调查春节联欢晚会的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
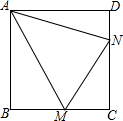 已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.
已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
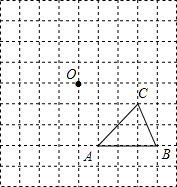 如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com