
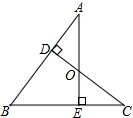
 如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )
如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )| A. | AO=CO | B. | DO=EO | C. | AD=CE | D. | ∠A=∠C |
分析 由三角形全等的判定方法AAS、ASA得出A、B、C能证明△AOD≌△COE,D不能.
解答 解:A能证明△AOD≌△COE;理由:
在△AOD和△COE中,$\left\{\begin{array}{l}{∠ADO=∠CEO}&{\;}\\{∠AOD=∠COE}&{\;}\\{AO=CO}&{\;}\end{array}\right.$,
∴△AOD≌△COE(AAS);
B能证明△AOD≌△COE;理由:
在△AOD和△COE中,$\left\{\begin{array}{l}{∠ADO=∠CEO}&{\;}\\{DO=EO}&{\;}\\{∠AOD=∠COE}&{\;}\end{array}\right.$,
∴△AOD≌△COE(ASA);
C能证明△AOD≌△COE;理由同A;
D不正确;三角形全等必须有对应边相等,只有角相等不一定全等;
故选:D.
点评 本题考查了三角形全等的判定方法;三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,熟练掌握三角形全等的判定方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800 |
| 第二周 | 4台 | 10台 | 3100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
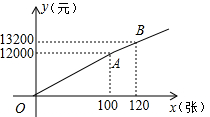 为了发展本地足球运动,在体育局的策划下,市体育馆将举行明星足球邀请赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):方案一:提供8 000元赞助后,每张票的票价为50元,方案二:票价按下图中的折线OAB所表示的函数关系确定.
为了发展本地足球运动,在体育局的策划下,市体育馆将举行明星足球邀请赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):方案一:提供8 000元赞助后,每张票的票价为50元,方案二:票价按下图中的折线OAB所表示的函数关系确定.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com