
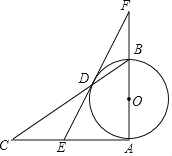
【题目】如图,已知AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.
(1)求证:DE为⊙O的切线.
(2)若BF=2,tan∠BDF=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析 (2)3
【解析】
(1)连AD,OD,则∠ADB=∠ADC=90°,由直角三角形斜边上的中线性质得:EA=ED,∠EDA=∠EAD,由等腰三角形的性质得:∠ODA=∠OAD,证得∠EDO=∠EAO,即可得出结论;
(2)由切线的性质得:∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°,证出∠FDB=∠FAD,∠F为公共角,得出△FDB∽△FAD,由对应边成比例即可得出结论.
(1)证明:连AD,OD,如图所示:
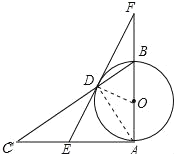
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
∵E是AC的中点,
∴EA=ED,
∴∠EDA=∠EAD,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠EDO=∠EAO,
∵AB⊥AC,
∴∠EAO=90°,
∴∠EDO=90°,
∴DE为⊙O的切线;
(2)解:∵DE为⊙O的切线,
∴∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠FDB=∠FAD,
∵tan∠BDF=![]() ,
,
∴![]() =
=![]()
又∵∠F为公共角,
∴△FDB∽△FAD,
∴![]() =
=![]() ,
,
∵BF=2
∴![]() =
=![]()
∴DF=4,AF=8
∴AB=8﹣2=6
∴⊙O的半径是3.


科目:初中数学 来源: 题型:
【题目】对于抛物线y=﹣(x+2)2+3,下列结论中正确结论的个数为( )
①抛物线的开口向下; ②对称轴是直线x=﹣2;
③图象不经过第一象限; ④当x>2时,y随x的增大而减小.
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的试验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )
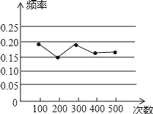
A. 任意买一张电影票,座位号是2的倍数的概率
B. 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C. 抛一个质地均匀的正方体骰子,落下后朝上的面点数是3
D. 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
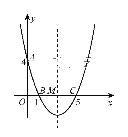
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
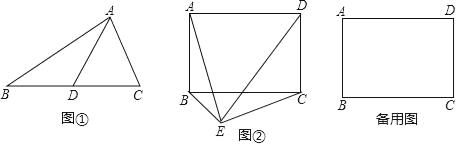
【题目】小儒在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考:
(1)他认为该定理有逆定理,即“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立,你能帮小儒证明一下吗?如图①,在△ABC中,AD是BC边上的中线,若AD=BD=CD,求证:∠BAC=90°.
(2)接下来,小儒又遇到一个问题:如图②,已知矩形ABCD,如果在矩形外存在一点E,使得AE⊥CE,求证:BE⊥DE,请你作出证明,可以直接用到第(1)问的结论.
(3)在第(2)问的条件下,如果△AED恰好是等边三角形,直接用等式表示出此时矩形的两条邻边AB与BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点A(c,-2),
的图象经过点A(c,-2),![]() 。求证:这个二次函数图象的对称轴是x=3.题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
。求证:这个二次函数图象的对称轴是x=3.题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
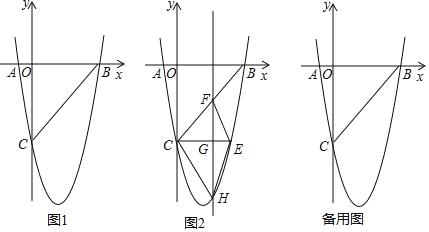
【题目】如图 1,在平面直角坐标系中,已知抛物线 y=ax2+bx﹣5 与 x 轴交于 A(﹣1,0),B(5, 0)两点,与 y 轴交于点 C.
(1)求抛物线的函数表达式;
(2)若点 D 是 y 轴上的一点,且以 B,C,D 为顶点的三角形与△ABC 相似,求点 D 的坐标;
(3)如图 2,CE∥x 轴与抛物线相交于点 E,点 H 是直线 CE 下方抛物线上的动点,过点 H且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形CHEF 的面积最大,求点 H 的坐标及最大面积;
(4)若点 K 为抛物线的顶点,点 M(4,m)是该抛物线上的一点,在 x 轴,y 轴上分别找点 P,Q,使四边形 PQKM 的周长最小,求出点 P,Q 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
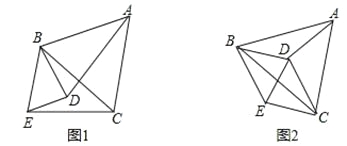
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com