【题目】已知二次函数
的图象经过点A（c,-2），
。求证：这个二次函数图象的对称轴是x=3.题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
（1）根据已知和结论中现有的信息，你能否求出题中的二次函数解析式？若能，请写出求解过程，并画出二次函数的图象；若不能，请说明理由.
（2）请你根据已有的信息，在原题中的矩形框中，填加一个适当的条件，把原题补充完整.
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案科目：初中数学 来源： 题型：
【题目】（2017·吉林）如图①，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水，28s时注满水槽．水槽内水面的高度y（cm）与注水时间x（s）之间的函数图象如图②所示．
（1）正方体的棱长为 cm；
（2）求线段AB对应的函数解析式，并写出自变量x的取值范围；
（3）如果将正方体铁块取出，又经过t（s）恰好将此水槽注满，直接写出t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
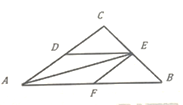
【题目】如图，在△ABC中，AB=3+
,∠B=45°，∠C=105°，点 D、E、F分别在AC、BC、AB上，且四边形ADEF为菱形，若点P是AE上一个动点，则PF+PB的最小值为___________ 。
查看答案和解析>>
科目：初中数学 来源： 题型：
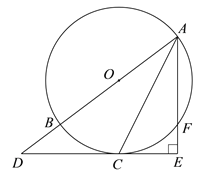
【题目】如图，AB为⊙O的直径，C、F为⊙O上两点，且点C为弧BF的中点，过点C作AF的垂线，交AF的延长线于点E，交AB的延长线于点D．
（1）求证：DE是⊙O的切线；
（2）如果半径的长为3，tanD=
，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
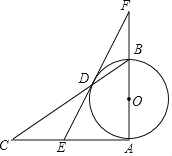
【题目】如图，已知AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，ED与AB的延长线相交于点F．
（1）求证：DE为⊙O的切线．
（2）若BF＝2，tan∠BDF＝
，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，E，F分别为BC，CD上的点，且AE⊥BF，垂足为G．
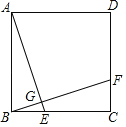
（1）求证：AE＝BF；（2）若BE＝
，AG＝2，求正方形的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：
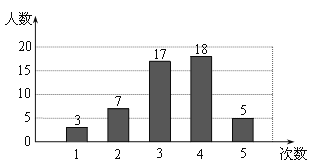
（Ⅰ）求这50个样本数据的平均数、众数和中位数；
（Ⅱ）根据样本数据，估算该校1200名学生共参加了多少次活动．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】兴发服装店老板用4500元购进一批某款T恤衫，由于深受顾客喜爱，很快售完，老板又用4950元购进第二批该款式T恤衫，所购数量与第一批相同，但每件进价比第一批多了9元．
（1）第一批该款式T恤衫每件进价是多少元？
（2）老板以每件120元的价格销售该款式T恤衫，当第二批T恤衫售出
时，出现了滞销，于是决定降价促销，若要使第二批的销售利润不低于650元，剩余的T恤衫每件售价至少要多少元？（利润=售价﹣进价）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用两种方法证明“圆的内接四边形对角互补”．
已知：如图①，四边形ABCD内接于⊙O．
求证：∠B＋∠D＝180°．
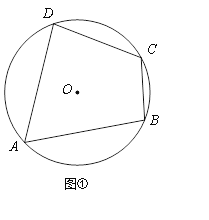
证法1：如图②，作直径DE交⊙O于点E，连接AE、CE．
∵DE是⊙O的直径，
∴ ．
∵∠DAE＋∠AEC＋∠DCE＋∠ADC＝360°，
∴∠AEC＋∠ADC＝360°－∠DAE－∠DCE＝360°－90°－90°＝180°．
∵∠B和∠AEC所对的弧是
，
∴ ．
∴∠B＋∠ADC＝180°．
请把证法1补充完整，并用不同的方法完成证法2．
证法2：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
