
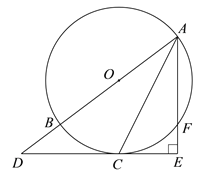
【题目】如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF的延长线于点E,交AB的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)如果半径的长为3,tanD=![]() ,求AE的长.
,求AE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OC,如图,由弧BC=弧CF得到∠BAC=∠FAC,加上∠OCA=∠OAC.则∠OCA=∠FAC,所以OC∥AE,从而得到OC⊥DE,然后根据切线的判定定理得到结论;
(2)先在Rt△OCD中利用正切定义计算出CD=4,再利用勾股定理计算出OD=5,则sinD=![]() ,然后在Rt△ADE中利用正弦的定义可求出AE的长.
,然后在Rt△ADE中利用正弦的定义可求出AE的长.
试题解析:解:(1)连接OC,如图.∵点C为弧BF的中点,∴弧BC=弧CF,∴∠BAC=∠FAC.∵OA=OC,∴∠OCA=∠OAC,∴∠OCA=∠FAC,∴OC∥AE.∵AE⊥DE,∴OC⊥DE,∴DE是⊙O的切线;
(2)在Rt△OCD中,∵tanD=![]() ,OC=3,∴CD=4,∴OD=
,OC=3,∴CD=4,∴OD=![]() =5,∴AD=OD+AO=8.在Rt△ADE中,∵sinD=
=5,∴AD=OD+AO=8.在Rt△ADE中,∵sinD=![]() ,∴AE=
,∴AE=![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
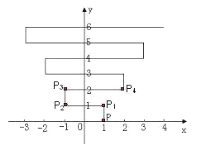
【题目】如下图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位…,依此规律跳动下去,点P第2019次跳动至点P2019的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
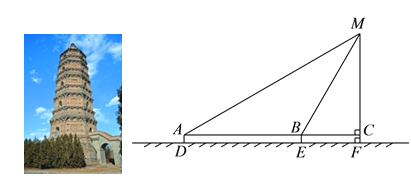
【题目】某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点![]() 用高
用高![]() 米的测角仪
米的测角仪![]() 测得塔顶
测得塔顶![]() 的仰角为
的仰角为![]() ,然后沿
,然后沿![]() 方向前行
方向前行![]() m到达点
m到达点![]() 处,在
处,在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() .请根据他们的测量数据求此塔
.请根据他们的测量数据求此塔![]() 的高.(结果精确到
的高.(结果精确到![]() m,参考数据:
m,参考数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)在数轴上表示下列各数:0,–2.5,![]() ,–2,+5,
,–2,+5,![]() .
.
![]()
(2)将上列各数用“<”连接起来:___________ _____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣|﹣![]() |,0,
|,0,![]() ,﹣(﹣3.14),2006,﹣(+5),+1.88,
,﹣(﹣3.14),2006,﹣(+5),+1.88,
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)分数集合:{ …}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com