
【题目】在开展“学雷锋社会实践”活动中,某校为了解全校1200名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如下:
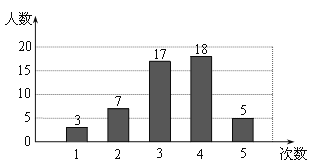
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估算该校1200名学生共参加了多少次活动.
【答案】
【解析】解:(Ⅰ)观察条形统计图,可知这组样本数据的平均数是:
![]() 。
。
∵在这组样本数据中,4出现了18次,出现的次数最多,
∴这组数据的众数是4。
∵将这组样本数据按从小到大的顺序排列,其中处在中间的两个数都是3,
∴这组数据的中位数是3。
(Ⅱ)∵这组样本数据的平均数是3.3,
∴估计全校1200人参加活动次数的总体平均数是3.3,
∴3.3×1200=3960。
∴估计该校学生共参加活动约为3960次
(Ⅰ)根据加权平均数的公式可以计算出平均数;根据众数的定义:一组数据中出现次数最多的数据叫做众数,中位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数,即可求出众数与中位数。
(Ⅱ)利用样本估计总体的方法,用样本中的平均数×1200即可


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
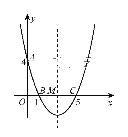
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点A(c,-2),
的图象经过点A(c,-2),![]() 。求证:这个二次函数图象的对称轴是x=3.题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
。求证:这个二次函数图象的对称轴是x=3.题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 A 在函数y1=-![]() (x>0)的图象上,点 B 在直线 y2=kx+1+k(k 为常数,且 k≥0)上.若 A,B 两点关于原点对称,则称点 A,B 为函数 y1,y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点 B 在直线 y2=kx+1+k(k 为常数,且 k≥0)上.若 A,B 两点关于原点对称,则称点 A,B 为函数 y1,y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对B.只有1对
C.只有2对D.有2对或3对
查看答案和解析>>
科目:初中数学 来源: 题型:
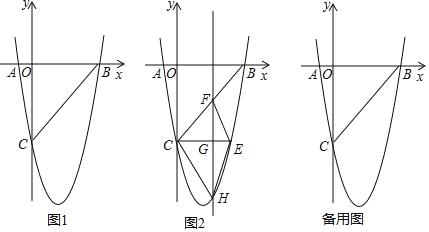
【题目】如图 1,在平面直角坐标系中,已知抛物线 y=ax2+bx﹣5 与 x 轴交于 A(﹣1,0),B(5, 0)两点,与 y 轴交于点 C.
(1)求抛物线的函数表达式;
(2)若点 D 是 y 轴上的一点,且以 B,C,D 为顶点的三角形与△ABC 相似,求点 D 的坐标;
(3)如图 2,CE∥x 轴与抛物线相交于点 E,点 H 是直线 CE 下方抛物线上的动点,过点 H且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形CHEF 的面积最大,求点 H 的坐标及最大面积;
(4)若点 K 为抛物线的顶点,点 M(4,m)是该抛物线上的一点,在 x 轴,y 轴上分别找点 P,Q,使四边形 PQKM 的周长最小,求出点 P,Q 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标.
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM +CN =BD.
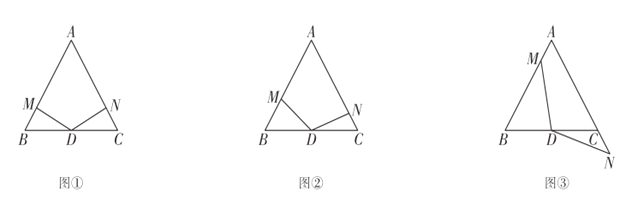
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB.上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com