
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.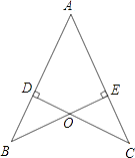
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,“赵爽弦图”由4个全等的直角三角形拼成,在Rt△ABC中,∠ACB=90°,AC=b,BC=a,请你利用这个图形解决下列问题:
(1)证明勾股定理;
(2)说明a2+b2≥2ab及其等号成立的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题一定成立的是 ( )
①对顶角相等; ②同位角相等,两直线平行;③全等三角形的周长相等;④面积相等的两个三角形全等
A. ①②③ B. ①④ C. ②④ D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式﹣5a2bc+3ab2﹣abc各项提公因式后,另一个因式是( )
A.5ac﹣3ab+c
B.5bc﹣3b+c
C.﹣5ac+3b+c
D.﹣5bc+3b+c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com