
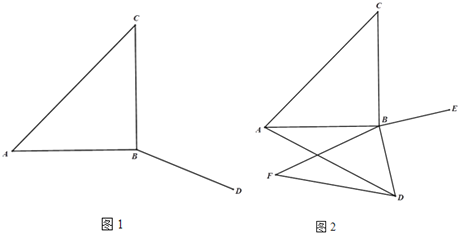
【题目】已知:在等腰直角三角形ABC中,AB=BC,∠ABC=90°.D是平面上一点,连结BD.将线段BD绕点B逆时针旋转90°得到线段BE,连结AE,CD.
(1)在图1中补全图形,并证明:AE⊥CD.
(2)当点D在平面上运动时,请猜测线段AD,CE,AB,BD之间的数量关系.
(3)如图2,作点A关于直线BE的对称点F,连结AD,DF,BF.若AB=11,BD=7,AD=14,求线段DF的长度.
【答案】(1)详见解析;(2)![]() ;(3)DF=12
;(3)DF=12
【解析】
(1)由旋转的性质得到∠DBE=90°,BD=BE,进而可得∠ABE=∠CBD,即可证明△ABE≌△CBD,由全等三角形对应角相等得到∠EAB=∠DCB.在△AMB和△CMN,根据对顶角相等和三角形内角和定理即可得到∠CNM=90°,即可得出结论;
(2)连接ED.在Rt△CNE、Rt△AND、Rt△ANC、Rt△DNE中,分别利用勾股定理即可得出结论.
(3)延长EB到G.由A和F关于直线BE对称,得到∠ABG=∠FBG,AB=BF,进而得到BC=BF.根据邓娇的余角相等得到∠CBE=∠FBD,即可证明△CBE≌△FBD,根据全等三角形对应边相等得到CE=FD.由(2)的结论可求出CE的长,等量代换即可得出结论.
(1)作图见图1.
∵将线段BD绕点B逆时针旋转90° 得到线段BE,
∴∠DBE=90°,BD=BE.
∵∠ABC=90°,
∴∠ABE=∠CBD.
在△ABE和△CBD中,∵AB=BC,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD,
∴∠EAB=∠DCB.
∵∠AMB=∠CMN,
∴∠CNM=∠ABM=90°,
∴AE⊥CD;
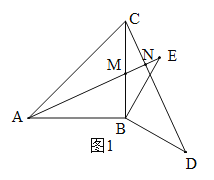
(2)![]() .理由如下:
.理由如下:
连接ED,如图2.
∵AE⊥CD,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
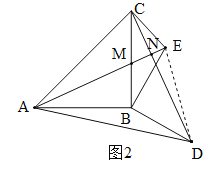
(3)延长EB到G,如图3.
∵A和F关于直线BE对称,
∴∠ABG=∠FBG,AB=BF.
∵AB=BC,
∴BC=BF.
∵∠ABC=∠DBE=90°,
∴∠ABG+∠CBE=90°,∠FBG+∠FBD=90°,
∴∠CBE=∠FBD.
在△CBE和△FBD中,∵CB=FB,∠CBE=∠FBD,BE=BD,
∴△CBE≌△FBD,
∴CE=FD.
由(2)可知:![]() ,
,
∴![]() ,
,
∴CE=12,
∴DF=CE=12.


科目:初中数学 来源: 题型:
【题目】小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与函数
的图象与函数![]() (
(![]() )的图象相交于点
)的图象相交于点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() .点
.点![]() 是线段
是线段![]() 上一点,
上一点,![]() 与
与![]() 的面积比为2:3.
的面积比为2:3.
(1)![]() ,
,![]() ;
;
(2)求点![]() 的坐标;
的坐标;
(3)若将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,其中
,其中![]() 的对应点是
的对应点是![]() ,
,![]() 的对应点是
的对应点是![]() ,当点
,当点![]() 落在
落在![]() 轴正半轴上,判断点
轴正半轴上,判断点![]() 是否落在函数
是否落在函数![]() (
(![]() )的图象上,并说明理由.
)的图象上,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,BD是角平分线,以点D为圆心,DA为半径的⊙D与AC相交于点E
(1)求证:BC是⊙D的切线;
(2)若AB=5,BC=13,求CE的长.
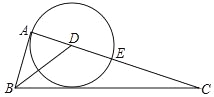
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2–kx+k–1(k>2).
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若ΔOAC的面积是![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组根据学习函数的经验,对分段函数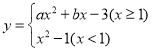 的图象与性质进行了探究,请补充完整以下的探究过程.
的图象与性质进行了探究,请补充完整以下的探究过程.
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | -1 | 0 | 1 | 0 | -3 | … |
(1)填空:a= .b= .
(2)①根据上述表格数据补全函数图象;
②该函数图象是轴对称图形还是中心对称图形?
(3)若直线![]() 与该函数图象有三个交点,求t的取值范围.
与该函数图象有三个交点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,建筑物AB的高为6cm,在其正东方向有个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A、塔项C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() =1.73,精确到0.1m)
=1.73,精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
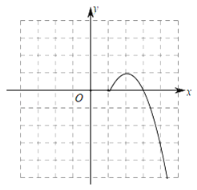
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
(2)将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
(3)求(2)中的点C旋转到点C2时,点C经过的路径长(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com