
【题目】已知二次函数y=x2–kx+k–1(k>2).
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若ΔOAC的面积是![]() ,求抛物线的解析式.
,求抛物线的解析式.
【答案】(1)详见解析;(2)y=x2-4x+3
【解析】
(1)先计算判别式的值得到△=(k﹣2)2,利用k>2,可判断△>0,于是根据△=b2﹣4ac>0时,抛物线与x轴有2个交点即可得到结论;
(2)根据抛物线与x轴的交点问题,解方程x2﹣kx+k﹣1=0得x=k﹣1或x=1,利用k>2,点A在点B的左侧得到A(1,0),B(k﹣1,0),再表示出C(0,k﹣1),然后根据ΔOAC的面积是![]() ,解方程求出k即可得到抛物线的表达式.
,解方程求出k即可得到抛物线的表达式.
(1)∵△=(﹣k)2﹣4×1×(k﹣1)=(k﹣2)2,
又∵k>2,
∴(k﹣2)2>0,即△>0,
∴抛物线y=x2﹣kx+k﹣1与x轴必有两个交点;
(2)∵抛物线y=x2﹣kx+k﹣1与x轴交于A、B两点,
∴令y=0,有x2﹣kx+k﹣1=0,解得:x=k﹣1或x=1.
∵k>2,点A在点B的左侧,
∴A(1,0),B(k﹣1,0).
∵抛物线与y轴交于点C,
∴C(0,k﹣1).
∵![]() ,
,
∴k-1=3,解得:k=4,
∴抛物线的表达式为y=x2﹣4x+3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
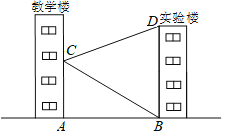
【题目】如图,学校教学楼对面是一幢实验楼,小朱在教学楼的窗口C测得实验楼顶部D的仰角为20°,实验楼底部B的俯角为30°,量得教学楼与实验楼之间的距离AB=30m.求实验楼的高BD.(结果精确到1m.参考数据tan20°≈0.36,sin20°≈0.34,cos20°≈0.94,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,顶点为
两点,顶点为![]() ,设点
,设点![]() 是
是![]() 轴的正半轴上一点,将抛物线
轴的正半轴上一点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
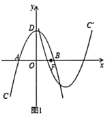
![]() 求抛物线
求抛物线![]() 的函数表达式:
的函数表达式:
![]() 若抛物线
若抛物线![]() 与抛物线
与抛物线![]() 在
在![]() 轴的右侧有两个不同的公共点,求
轴的右侧有两个不同的公共点,求![]() 的取值范围.
的取值范围.
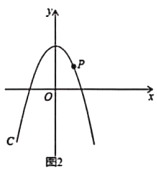
![]() 如图2,
如图2,![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,它到两坐标轴的距离相等,点
上一点,它到两坐标轴的距离相等,点![]() 在抛物线
在抛物线![]() 上的对应点
上的对应点![]() ,设
,设![]() 是
是![]() 上的动点,
上的动点,![]() 是
是![]() 上的动点,试探究四边形
上的动点,试探究四边形![]() 能否成为正方形?若能,求出
能否成为正方形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
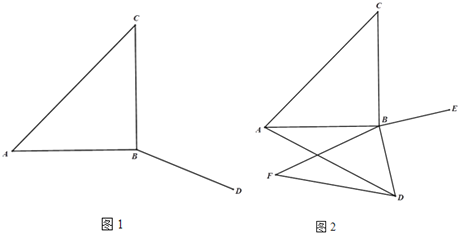
【题目】已知:在等腰直角三角形ABC中,AB=BC,∠ABC=90°.D是平面上一点,连结BD.将线段BD绕点B逆时针旋转90°得到线段BE,连结AE,CD.
(1)在图1中补全图形,并证明:AE⊥CD.
(2)当点D在平面上运动时,请猜测线段AD,CE,AB,BD之间的数量关系.
(3)如图2,作点A关于直线BE的对称点F,连结AD,DF,BF.若AB=11,BD=7,AD=14,求线段DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,E为AC上一点,直线ED与AB延长线交于点F,若∠CDE=∠DAC,AC=12.
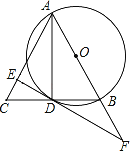
(1)求⊙O半径;
(2)求证:DE为⊙O的切线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
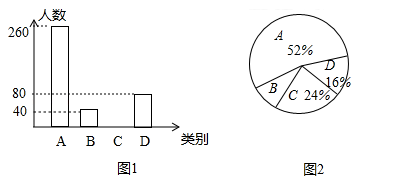
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户C类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com