
【题目】某烟机零件加工车间,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.
(l)求乙组加工零件的数量y与时间t之间的函数关系式.
(2)求甲组加工零件总量a.

【答案】(1) y=120x﹣600;(2)280个.
【解析】分析:(1)由图象可知,乙组加工零件的数量y与时间t之间是一次函数的关系,函数图象过点(5,0),(8,360),用待定系数法求y与t之间的函数关系式;(2)把x=7代入(1)所求的函数关系式求出x=7时,y的值,即可得到甲在4时到8时之间每小时加工的零件数量,由此求出8小时时加工的零件数量.
详解:解:(1)当0≤t<5时,y=0,
当5≤t≤8时,设y与时间t之间的函数关系式为:y=kx+b,
将(5,0),(8,360)代入得:![]() ,解得:
,解得:![]() ,
,
∴y与时间t之间的函数关系式为:y=120x﹣600;
(2)∵当t=7时,y=120×7﹣600=240,
4时到8时之间每小时加工的零件数量为(240﹣120)÷(7﹣4)=40.
∴a=120+40×(8﹣4)=280(个).


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1 100 | 1 400 |
销售价格(元) | 今年的销售价格 | 2 000 |
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y厘米.

小新根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y(cm) | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
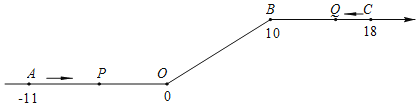
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB和CD交于O,∠AOC的度数为x,∠BOE=90°OF平分∠AOD.

(1)当x=20°时,则∠EOC=_____度;∠FOD=_____度.
(2)当x=60°时,射线OE′从OE开始以10°/秒的速度绕点O逆时针转动,同时射线OF′从OF开始以8°/秒的速度绕点O顺时针转动,当射线OE转动一周时射线OF′也停正转动,求至少经过多少秒射线OE′与射线OF重合?
(3)在(2)的条件下,射线OE′在转动一周的过程中,当∠E′OF′=90°时,请直接写出射线OE′ 转动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.

(1)如图①,若∠BAC=23°,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究位似问题时,甲、乙同学的说法如下:
甲:如图①,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(0,2).


图① 图②
乙:如图②,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(4,0).
对于两人的观点,下列说法正确的是( )
A. 两人都对 B. 两人都不对 C. 甲对乙不对 D. 甲不对乙对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com