
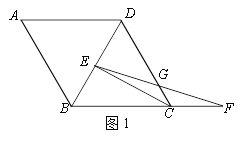
【题目】等腰△ABD中,AD=BD,将△ABD绕腰BD的中点顺时针旋转180°,得到△CDB,CE平分∠BCD交BD于点E,在BC的延长线上取点F,使CF=DE,连接EF交CD于点G.
(1)如图1,∠A=60°,AB=4,求CF的长;
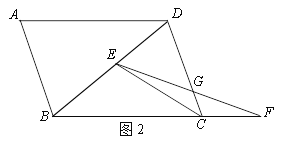
(2)如图2,求证:DE=2CG.
【答案】(1)CF=2;(2)详见解析
【解析】
(1)先证明△ABD是等边三角形,再根据旋转的性质得到△CBD是等边三角形,根据等腰三角形的三线合一的性质即可得到CF的长;
(2)过点E作EM∥BC,交CD于点M,利用平行线的性质及等腰三角形的性质得到DE=EM=CF,由此证明△EMG≌△FCG,再利用角平分线的性质即可得到结论.
(1)解:∵AD=BD,∠A=60°
∴△ABD是等边三角形
∴∠ADB=60°,BD =4
由旋转性质知,得△ABD≌△CDB
∴△CBD是等边三角形
且CE平分∠BCD
∴BE=DE=2
∵CF=DE
∴CF=2
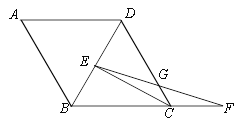
(2)过点E作EM∥BC,交CD于点M,
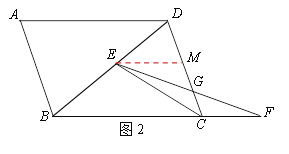
∴∠DME=∠DCB, ∠MEG=∠F, ∠ECB=∠MEC,
∵BD=CB,
∴∠BDC=∠BCD=∠DME,
∴DE=EM=CF,
在△EMG和△FCG中
 ,
,
∴△EMG≌△FCG,
∴MG=CG,
∵CE平分∠BCD,
∴∠ECB=∠ECM=∠MEC,
∴EM=MC=2CG,
∴DE=2GC.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
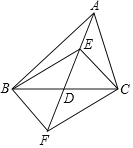
【题目】在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若AB=AC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是_____(填序号).
①在同一平面内,a,b,c为直线,若a⊥b,b⊥c,则a∥c;
②“若ac>bc,则a>b”的逆命题是真命题;
③若点M(a,2)与N(1,b)关于x轴对称,则a+b=﹣1;
④![]() 的整数部分是a,小数部分是b,则ab=3
的整数部分是a,小数部分是b,则ab=3![]() ﹣3.
﹣3.
查看答案和解析>>
科目:初中数学 来源: 题型:
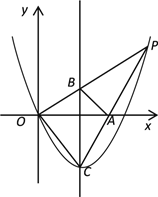
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被哦感染.
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
(3)![]() 轮(
轮(![]() 为正整数)感染后,被感染的电脑有________台.
为正整数)感染后,被感染的电脑有________台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,BD平分∠ABC,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好经过点D.
(1)求证:直线AC是⊙O的切线;
(2)若∠A=30°,⊙O的半径是2,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中ac≠0,a≠c.下列四个结论中:正确的个数有( )
①如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根;
②如果ac<0,方程M、N都有两个不相等的实数根;
③如果2是方程M的一个根,那么![]() 是方程N的一个根;
是方程N的一个根;
④如果方程M和方程N有一个相同的根,那么这个根必是x=1.
A.4个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
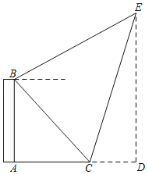
【题目】如图所示,小明所住高楼AB高为100米,楼旁有一座坡比为3:1的山坡CE,小明想知道山坡的高度,于是小明来到楼顶B俯视坡底C,测得俯角为45°,仰视坡项E,测得仰角为27°,请根据小明提供的信息,帮小明求出斜坡CE的高度ED的值.(结果均精确到0.1米.参考数据:sin27°≈0.45,cos37°≈0.89,tan27°≈0.51)( )
A.151.1米B.168.7米C.171.6米D.181.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为450 ,然后他沿着正对树PQ的方向前进10m到达B点处,此时测得树顶P和树底Q的仰角分别是600和300,设PQ垂直于AB,且垂足为C.
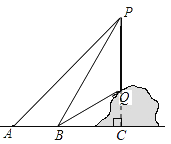
(1)求∠BPQ的度数;
(2)求树PQ的高度(结果精确到0.1m, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com