
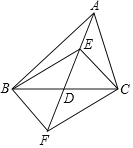
【题目】在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若AB=AC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
【答案】(1)证明见解析;(2)四边形BFCE是菱形,证明见解析.
【解析】
(1)由平行线的性质得出∠ECD=∠FBD,∠DEC=∠DFB,然后再加上由中点得出的BD=DC,即可利用AAS证明△BDF≌△EDC;
(2)先根据等腰三角形的三线合一证明AD⊥BC,然后由(1)中的可得出DE=DF,DB=DC,最后利用对角线互相平分且互相垂直的四边形为菱形即可证明四边形BFCE是菱形.
(1)∵CE∥BF,
∴∠ECD=∠FBD,∠DEC=∠DFB;
又∵D是BC的中点,
∴BD=DC,
∴△BDF≌△EDC(AAS);
(2)四边形BFCE是菱形.证明如下:
∵AB=AC,
∴△ABC是等腰三角形;
又∵BD=DC,
∴AD⊥BC,
由(1)知:△BDF≌△EDC,
则DE=DF,DB=DC;
∴四边形BFCE是菱形.


科目:初中数学 来源: 题型:
【题目】数学问题:如何计算平面直角坐标系中任意两点之间的距离?
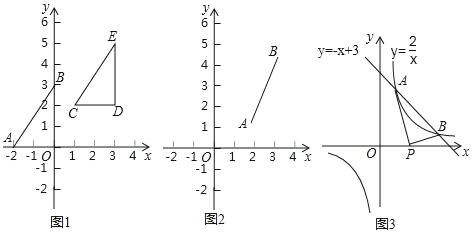
探究问题:
为解决上面的问题,我们从最简单的问题进行研究.
探究一:在图1中,已知线段AB,A(﹣2,0),B(0,3),写出线段AO的长,BO的长,所以线段AB的长为多少;把Rt△AOB向右平移3个单位,再向上平移2个单位,得到Rt△CDE,写出Rt△CDE的顶点坐标C,D,E,此时线段CD的长为多少,DE的长为多少,所以线段CE的长为多少.
探究二:在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB的长(用含a,b,c,d的代数式表示,不必证明).
归纳总结:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(x1,y1),B(x2,y2)时线段AB的长为多少(用含x1,y1,x2,y2的代数式表示,不必证明).
拓展与应用:
运用在图3中,一次函数y=﹣x+3与反比例函数y=![]() 的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
①求线段AB的长;
②若点P是x轴上动点,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
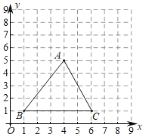
【题目】如图,由边长为1的小正方形构成的网格中,每个小正方形的顶点叫做格点,![]() 的顶点在格点上.
的顶点在格点上.
(1)直接写出![]() 的面积为 ;
的面积为 ;
(2)请用无刻度的直尺画出将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 角后得到的线段
角后得到的线段![]() ,并写出点
,并写出点![]() 的坐标为 ;
的坐标为 ;
(3)若一个多边形各点都不在⊙M外,则称⊙M全覆盖这个5多边形,已知点![]() ,⊙M全覆盖四边形
,⊙M全覆盖四边形![]() ,则⊙M的直径最小为
,则⊙M的直径最小为
查看答案和解析>>
科目:初中数学 来源: 题型:
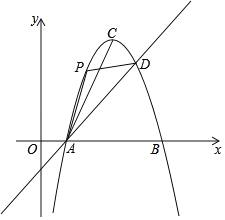
【题目】如图,直线y=x﹣1与抛物线y=﹣x2+6x﹣5相交于A、D两点.抛物线的顶点为C,连结AC.
(1)求A,D两点的坐标;
(2)点P为该抛物线上一动点(与点A、D不重合),连接PA、PD.
①当点P的横坐标为2时,求△PAD的面积;
②当∠PDA=∠CAD时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种产品,其标价比进价每件多![]() 元,且商店用
元,且商店用![]() 元购进这种商品的数量和这种商品
元购进这种商品的数量和这种商品![]() 元的销售额所售出的件数相同.
元的销售额所售出的件数相同.
![]() 求这种商品的进价及标价;
求这种商品的进价及标价;
![]() 经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出
经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出![]() 件,每涨价
件,每涨价![]() 元,则少卖出
元,则少卖出![]() 件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
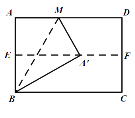
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM,若矩形纸片的宽AB=4,则折痕BM的长为( )
A.![]() B.
B.![]() C.8D.
C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
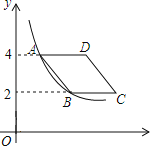
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
A. 2B. 3C. 4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
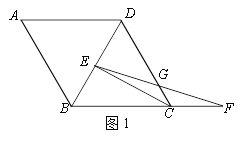
【题目】等腰△ABD中,AD=BD,将△ABD绕腰BD的中点顺时针旋转180°,得到△CDB,CE平分∠BCD交BD于点E,在BC的延长线上取点F,使CF=DE,连接EF交CD于点G.
(1)如图1,∠A=60°,AB=4,求CF的长;
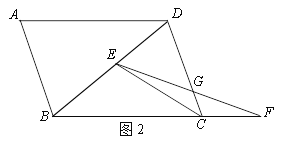
(2)如图2,求证:DE=2CG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com