
【题目】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被哦感染.
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
(3)![]() 轮(
轮(![]() 为正整数)感染后,被感染的电脑有________台.
为正整数)感染后,被感染的电脑有________台.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某商店经销一种产品,其标价比进价每件多![]() 元,且商店用
元,且商店用![]() 元购进这种商品的数量和这种商品
元购进这种商品的数量和这种商品![]() 元的销售额所售出的件数相同.
元的销售额所售出的件数相同.
![]() 求这种商品的进价及标价;
求这种商品的进价及标价;
![]() 经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出
经过--段时间的销售,商店发现,以标价出售这种商品,每天可售出![]() 件,每涨价
件,每涨价![]() 元,则少卖出
元,则少卖出![]() 件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车驾驶员坐在驾驶座位上,其视线观察不到的地方叫“汽车盲区”.如图是一辆汽车的“车头盲区”示意图,其中AC⊥BC,DE⊥BC,驾驶员所处位置的高度AC为1.4米,驾驶员座位AC与车头DE之间距离为2米,当驾驶员从A点观察车头D点时,其视线的俯角为12°,点A、D、B在同一直线上.
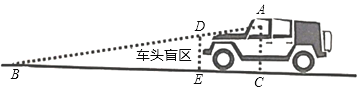
(1)请直接写出∠ABC的度数;
(2)求“车头盲区”点B、E之间的距离.(结果精确到0.1米)参考数据:sin12°=0.20,cas12°=0.99,tan12°=0.21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABD中,AD=BD,将△ABD绕腰BD的中点顺时针旋转180°,得到△CDB,CE平分∠BCD交BD于点E,在BC的延长线上取点F,使CF=DE,连接EF交CD于点G.
(1)如图1,∠A=60°,AB=4,求CF的长;
(2)如图2,求证:DE=2CG.
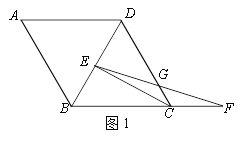
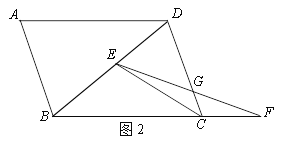
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°.
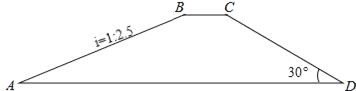
(1)求坝底AD的长度(结果精确到1米);
(2)若坝长100米,求建筑这个大坝需要的土石料(参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距30千米,已知甲、乙两人分别骑自行车和摩托车从
两地相距30千米,已知甲、乙两人分别骑自行车和摩托车从![]() 地出发前往
地出发前往![]() 地,途中乙因修车耽误了些时间,然后又继续赶路.图5中的线段
地,途中乙因修车耽误了些时间,然后又继续赶路.图5中的线段![]() 和折线
和折线![]() 分别反映了甲、乙两人所行的路程
分别反映了甲、乙两人所行的路程![]() (千米)与时间
(千米)与时间![]() (分)的函数关系,根据图像提供的信息回答下列问题:
(分)的函数关系,根据图像提供的信息回答下列问题:
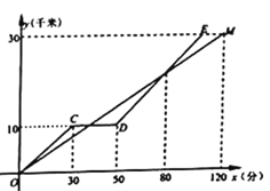
(1)甲骑自行车的速度是_________千米/分钟;
(2)两人第二次相遇时距离![]() 地________千米;
地________千米;
(3)线段![]() 反映了乙修好车后所行的路程
反映了乙修好车后所行的路程![]() (千米)与时间
(千米)与时间![]() (分)的函数关系.请求出线段
(分)的函数关系.请求出线段![]() 的表达式及其定义域.
的表达式及其定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;求x为何值时y的值为1920?
(2)每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com