
【题目】如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠A=∠B=∠C=∠D=90°)
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,求出BE的长.(用含x的代数式表式)

【答案】(1)证明见解析;(2))△PHD的周长不变为定值8,证明见解析;(3)![]()
【解析】试题分析:(1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;
(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8;
(3)利用已知得出△EFM≌△BPA,进而利用在Rt△APE中,(4BE)2+x2=BE2即可求出用含x的代数式表示的BE的长.
解: (1)如图1,
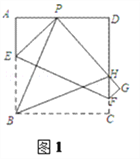
∵PE=BE,
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH∠EPB=∠EBC∠EBP.
即∠PBC=∠BPH.
∵AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)△PHD的周长不变为定值8.
证明:如图2,过B作BQ⊥PH,垂足为Q.
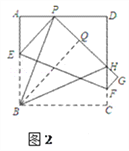
由(1)知∠APB=∠BPH,
∵∠A=∠BQP=90°,BP=BP,
∴△ABP≌△QBP.
∴AP=QP,AB=BQ.
∵AB=BC,
∴BC=BQ.
∵∠C=∠BQH=90°,BH=BH,
∴△BCH≌△BQH.
∴CH=QH.
∴△PHD的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8.
(3)如图3,过F作FM⊥AB,垂足为M,则FM=BC=AB.
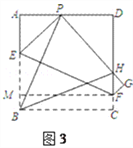
∵EF为折痕,
∴EF⊥BP.
∴∠EFM+∠MEF=∠ABP+∠BEF=90°,
∴∠EFM=∠ABP.
又∵∠A=∠EMF=90°,
∴△EFM≌△BPA.
∴EM=AP=x.
∴在Rt△APE中,
(4BE)2+x2=BE2.
解得: ![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=(m-3)x+m-8,y随x的增大而增大,
(1)求m的取值范围;
(2)如果这个一次函数又是正比例函数,求m的值;
(3)如果这个一次函数的图象经过一、三、四象限,试写一个m的值,不用写理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n +1)+(2n +3)=
(3)试计算:101 +103+…+197 +199.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.

(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;
(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
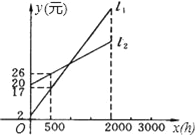
【题目】如图所示,l1和l2分别表示一种白炽灯和一种节能灯的费用y(元)与照明时间x(小时)的函数关系图象,假设两种灯的使用寿命都是2000小时,照明效果一样.(费用=灯的售价+电费)
(1)根据图象分别求出l1,l2的函数关系式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为a,b,c,记![]() ,那么三角形的面积为
,那么三角形的面积为![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: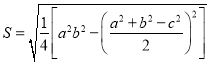 . ②
. ②
下面我们对公式②进行变形: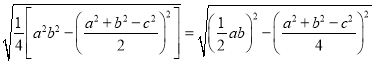
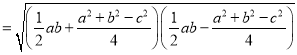
![]()
![]()
![]()
![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
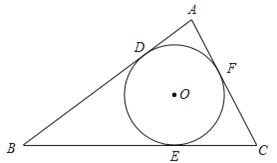
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com