
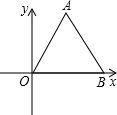
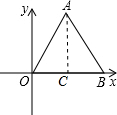
 如图,△AOB是边长为6的等边三角形,则OA所在直线方程为
如图,△AOB是边长为6的等边三角形,则OA所在直线方程为| 3 |
| OA2-OC2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
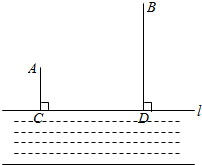 如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为
如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为查看答案和解析>>
科目:初中数学 来源: 题型:
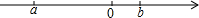 实数a、b在数轴上的位置如图所示,给出如下结论:①a+b>0;②b-a>0;③-a>b;④a>-b,⑤|a|>|b|>0.其中正确的结论是( )
实数a、b在数轴上的位置如图所示,给出如下结论:①a+b>0;②b-a>0;③-a>b;④a>-b,⑤|a|>|b|>0.其中正确的结论是( )| A、①②③ | B、②③④ |
| C、②③⑤ | D、②④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| a |
| a+1 |
| a2-2a |
| a2-4 |
| 1 |
| a+2 |
| a2-2ab+b2 |
| ab |
| a-b |
| a2 |
| 3 | 8 |
|
2
|
| 24 |
| 96 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com