
【题目】如图,△AOB是等腰直角三角形,直线BD∥OA,OB=OA=1,P是线段AB上一动点,过P点作MN∥OB,分别交OA、BD于M、N,PC⊥PO,交BD于点C.
(1)求证:OP=PC;
(2)当点C在射线BN上时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线BN上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形时的PM的值;如果不可能,请说明理由.

【答案】(1)证明见解析;(2)s=![]() m2﹣
m2﹣![]() m+1(0≤m≤
m+1(0≤m≤![]() ).(3) 0或
).(3) 0或![]() .
.
【解析】试题分析:(1)首先利用矩形的判定得出四边形OBNM为矩形,即可得出∠CPN=∠POM,进而得出△OPM≌△PCN,求出即可;
(2)利用S=S△OPB+S△PBC进而得出S与m的函数关系;
(3)利用①当点P与点A重合时,PC=BC=1,②如图②,当点C在OB下方,且PB=CB时,分别求出即可.
试题解析:(1)证明:如图①,△AOB是等腰直角三角形,AO=BO=1,
∴∠A=45°,∠AOB=90°,
直线BN∥OA,MN∥OB,
∴四边形OBNM为矩形,
∴MN=OB=1,∠PMO=∠CNP=90°
而∠AMP=90°,∠A=∠APM=∠BPN=45°,
∴OM=BN=PN,
∵∠OPC=90°,
∴∠OPM+∠CPN=90°,
又∵∠OPM+∠POM=90°,
∴∠CPN=∠POM,
在△OPM和△PCN中

∴△OPM≌△PCN(ASA),
∴OP=PC,
(2)解:∵AM=PM=APsin45°=![]() m,
m,
∴NC=PM=![]() m,∴BN=OM=PN=1﹣
m,∴BN=OM=PN=1﹣![]() m;
m;
∴BC=BN﹣NC=1﹣![]() m﹣
m﹣![]() m=1﹣
m=1﹣![]() m,
m,
S=S△OPB+S△PBC=![]() BOMO+
BOMO+![]() BCPN,
BCPN,
=![]() m2﹣
m2﹣![]() m+1(0≤m≤
m+1(0≤m≤![]() );
);
(3)解:△PBC可能为等腰三角形,
①当点P与点A重合时,PC=BC=1,此时PM=0,
②如图②,当点C在OB下方,且PB=CB时,
有OM=BN=PN=1﹣![]() m,
m,
∴BC=PB=![]() PN=
PN=![]() ﹣m,
﹣m,
∴NC=BN+BC=1﹣![]() m+
m+![]() ﹣m,
﹣m,
由(2)知:NC=PM=![]() m,
m,
∴1﹣![]() m+
m+![]() ﹣m=
﹣m=![]() m,
m,
∴m=1.
∴PM=![]() m=
m=![]() ;
;
∴使△PBC为等腰三角形时的PM的值为0或![]() .
.



科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.3a2b-a2b=2
B.单项式-x2的系数是-1
C.使式子(x+2)0有意义的x的取值范围是x≠0
D.若分式 ![]() 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
《九章算术》中有“盈不足术”的问题,原文如下:“今有共買羊,人出五,不足四十五;人出七,不足三.问人数、羊價各幾何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元.求人数和羊价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:

(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为等边三角形ABC内部一点,△ABP旋转后能与△CBP'重合.
(1)旋转中心是哪一点?旋转角是多少度?
(2)连接PP',△BPP'是什么三角形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
(1)①若将线段AB绕点O逆时针旋转90°得到线段A1B1 , 试在图中画出线段A1B1 .
②若线段A2B2与线段A1B1关于y轴对称,请画出线段A2B2 .
(2)若点P是此平面直角坐标系内的一点,当点A、B1、B2、P四边围成的四边形为平行四边形时,请你直接写出点P的坐标(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合.(在图3至图6中统一用F表示)
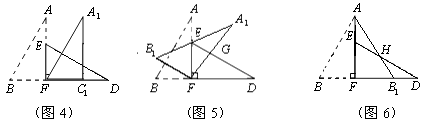
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请说明:AH=DH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com