
【题目】如图,![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() 点,点
点,点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 的面积是
的面积是![]() .
.

(1)求点![]() 坐标;
坐标;
(2)若动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位,设
个单位,设![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在![]() 的条件下,同时点Q从D点出发沿
的条件下,同时点Q从D点出发沿![]() 轴正方向以每秒
轴正方向以每秒![]() 个单位速度匀速运动,若点
个单位速度匀速运动,若点![]() 在过
在过![]() 点且平行于
点且平行于![]() 轴的直线上,当
轴的直线上,当![]() 为以
为以![]() 为直角边的等腰直角三角形时,求满足条件的
为直角边的等腰直角三角形时,求满足条件的![]() 值,并直接写出点
值,并直接写出点![]() 的坐标.
的坐标.
【答案】(1)点![]() 坐标为
坐标为![]() ;(2)当
;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;(3)当
;(3)当![]() 为以
为以![]() 为直角边的等腰直角三角形时,
为直角边的等腰直角三角形时,![]() 秒或
秒或![]() 秒或
秒或![]() 秒,点R对应的坐标分别为R(6,-17)或R(6,13)或R(6,
秒,点R对应的坐标分别为R(6,-17)或R(6,13)或R(6,![]() ).
).
【解析】
(1)由△ABD的面积即可求出AD的长度,从而求出点D的坐标;
(2)分两种情形①当0<t≤8时,②当t>8时,求出△PAC面积即可.
(3)分三种情形①如图1中,当∠QPR=90°,PQ=PR时,作RH⊥OP于H,②如图2中,当∠PQR=90°,QR=PQ时,③如图3中,当∠PQR=90°,QR=PQ时,利用全等三角形的性质列出方程即可解决.
解:(1)![]() 的面积是
的面积是![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() ;
;
(2)∵点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() 点,
点,
![]() 点
点![]() 坐标
坐标![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
(3)①如图1中,当![]() 时,作
时,作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,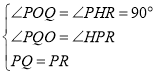
![]() ,
,
![]()
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]()
![]()
![]() ,
,
![]() ;
;
∴OQ=PH=2×10-9=11,
∴OH=6+11=17,
此时R(6,-17)
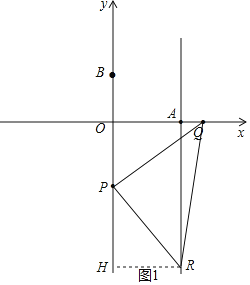
![]() 如图2中,当
如图2中,当![]() 时,
时,
![]()
![]() ,
,
在![]() 和
和![]() 中,
中,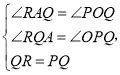
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
此时AR=OQ=2t-9=13
∴R(6,13)
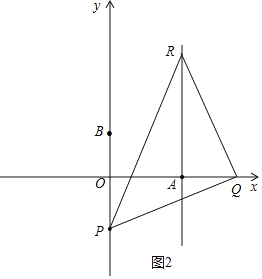
③如图3中,当∠PQR=90°时,QR=PQ时,
∵∠RQA+∠OQP=90°,
∠OQP+∠OPQ=90°,
∴∠RQA=∠OPQ,
在△ARQ与△OQP中,
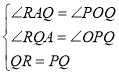 ,
,
∴△ARQ≌△OQP(AAS)
∴OP=AQ,
∴t-4=15-2t,
∴t=![]() ,
,
此时,AR=OQ=2t-9=![]() ,
,
∴R(6,![]() )
)

综上所述,当![]() 为以
为以![]() 为直角边的等腰直角三角形时,
为直角边的等腰直角三角形时,![]() 秒或
秒或![]() 秒或
秒或![]() 秒,点R对应的坐标分别为R(6,-17)或R(6,13)或R(6,
秒,点R对应的坐标分别为R(6,-17)或R(6,13)或R(6,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
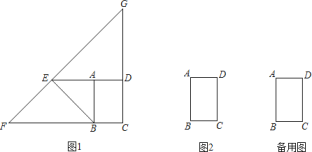
【题目】在矩形ABCD中,AB=3,AD=2,点E是射线DA上一点,连接EB,以点E为圆心EB长为半径画弧,交射线CB于点F,作射线FE与CD延长线交于点G.
(1)如图1,若DE=5,则∠DEG=______°;
(2)若∠BEF=60°,请在图2中补全图形,并求EG的长;
(3)若以E,F,B,D为顶点的四边形是平行四边形,此时EG的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
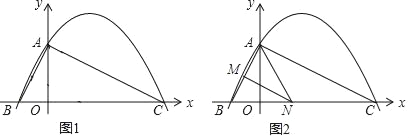
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
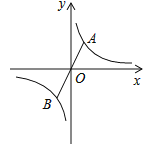
【题目】(2016湖北省荆门市)如图,已知点A(1,2)是反比例函数![]() 图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是______________.
图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
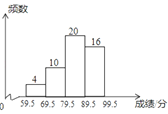
【题目】为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题:
(1)若抽取的成绩用扇形图来描述,则表示“第三组(79.5~89.5)”的扇形的圆心角为多少度;
(2)若成绩在90分以上(含90分)的同学可以获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且sin∠DCB=![]() .
.
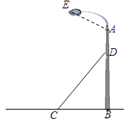
(1)求钢缆CD的长度。
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
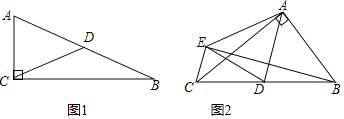
【题目】定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB,运用:如图2,△ABC中,∠BAC=90°,AB=2,AC=3,点D是BC的中点,将△ABD沿AD翻折得到△AED连接BE,CE,DE,则CE的长为_____.
AB,运用:如图2,△ABC中,∠BAC=90°,AB=2,AC=3,点D是BC的中点,将△ABD沿AD翻折得到△AED连接BE,CE,DE,则CE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com