
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),( ,
, ),…都是“梦之点”,显然,这样的“梦之点”有无数个.
),…都是“梦之点”,显然,这样的“梦之点”有无数个.
(1)若点P(2,m)是反比例函数y= (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+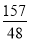 ,试求出t的取值范围.
,试求出t的取值范围.
(1)y= ;(2)当k≠
;(2)当k≠ 时,“梦之点”的坐标为(
时,“梦之点”的坐标为( ,
, );当k=
);当k= ,s=1时,“梦之点”有无数个;当k=
,s=1时,“梦之点”有无数个;当k= ,s≠1时,不存在“梦之点”;(3)t>
,s≠1时,不存在“梦之点”;(3)t>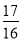 .
.
【解析】
试题分析:(1)先由“梦之点”的定义得出m=2,再将点P坐标代入y= ,运用待定系数法即可求出反比例函数的解析式;
,运用待定系数法即可求出反比例函数的解析式;
(2)假设函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”(x,x),则有x=3kx+s﹣1,整理得(3k﹣1)x=1﹣s,再分三种情况进行讨论即可;
(3)先将A(x1,x1),B(x2,x2)代入y=ax2+bx+1,得到ax12+(b﹣1)x1+1=0,ax22+(b﹣1)x2+1=0,根据方程的解的定义可知x1,x2是一元二次方程ax2+(b﹣1)x+1=0的两个根,由根与系数的关系可得x1+x2= ,x1•x2=
,x1•x2= ,则(x1﹣x2)2=(x1+x2)2﹣4x1•x2=
,则(x1﹣x2)2=(x1+x2)2﹣4x1•x2=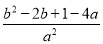 =4,整理得出b2﹣2b=(2a+1)2﹣2,则t=b2﹣2b+
=4,整理得出b2﹣2b=(2a+1)2﹣2,则t=b2﹣2b+ =(2a+1)2+
=(2a+1)2+ .再由﹣2<x1<2,|x1﹣x2|=2,得出﹣4<x2<4,﹣8<x1•x2<8,即﹣8<
.再由﹣2<x1<2,|x1﹣x2|=2,得出﹣4<x2<4,﹣8<x1•x2<8,即﹣8< <8,又a>0,解不等式组得出a>
<8,又a>0,解不等式组得出a>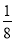 ,进而求出t的取值范围.
,进而求出t的取值范围.
试题解析:(1)∵点P(2,m)是“梦之点”,
∴m=2,
∵点P(2,2)在反比例函数y= (n为常数,n≠0)的图象上,
(n为常数,n≠0)的图象上,
∴n=2×2=4,
∴反比例函数的解析式为y= ;
;
(2)假设函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”(x,x),
则有x=3kx+s﹣1,
整理,得(3k﹣1)x=1﹣s,
当3k﹣1≠0,即k≠ 时,解得x=
时,解得x= ;
;
当3k﹣1=0,1﹣s=0,即k= ,s=1时,x有无穷多解;
,s=1时,x有无穷多解;
当3k﹣1=0,1﹣s≠0,即k= ,s≠1时,x无解;
,s≠1时,x无解;
综上所述,当k≠ 时,“梦之点”的坐标为(
时,“梦之点”的坐标为( ,
, );当k=
);当k= ,s=1时,“梦之点”有无数个;当k=
,s=1时,“梦之点”有无数个;当k= ,s≠1时,不存在“梦之点”;
,s≠1时,不存在“梦之点”;
(3)∵二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),
∴x1=ax12+bx1+1,x2=ax22+bx2+1,
∴ax12+(b﹣1)x1+1=0,ax22+(b﹣1)x2+1=0,
∴x1,x2是一元二次方程ax2+(b﹣1)x+1=0的两个不等实根,
∴x1+x2= ,x1•x2=
,x1•x2= ,
,
∴(x1﹣x2)2=(x1+x2)2﹣4x1•x2=( )2﹣4×
)2﹣4× =
=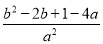 =4,
=4,
∴b2﹣2b=4a2+4a﹣1=(2a+1)2﹣2,
∴t=b2﹣2b+ =(2a+1)2﹣2+
=(2a+1)2﹣2+ =(2a+1)2+
=(2a+1)2+ .
.
∵﹣2<x1<2,|x1﹣x2|=2,
∴﹣4<x2<0或0<x2<4,
∴﹣4<x2<4,
∴﹣8<x1•x2<8,
∴﹣8< <8,
<8,
∵a>0,
∴a>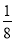
∴(2a+1)2+ >
> +
+ =
=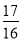 ,
,
∴t>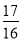 .
.
考点:二次函数综合题.


科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:填空题
有两块面积相同的蔬菜试验田,第一块使用原品种,第二块使用新品种,分别收获蔬菜1500千克和2100千克.已知第二块试验田每亩的产量比第一块多200千克.若设第一块试验田每亩的产量为x千克,则根据题意列出的方程是
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:解答题
如图,抛物线y=﹣ x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:选择题
把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )
A.y=﹣2(x+1)2+2 B.y=﹣2(x+1)2﹣2
C.y=﹣2(x﹣1)2+2 D.y=﹣2(x﹣1)2﹣2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:选择题
期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”,上面两位同学的话能反映处的统计量是( )
A.众数和平均数 B.平均数和中位数
C.众数和方差 D.众数和中位数
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南郴州卷)数学(解析版) 题型:解答题
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南邵阳卷)数学(解析版) 题型:选择题
地球的表面积约为511000000km2,用科学记数法表示正确的是( )

A.5.11×1010km2 B.5.11×108km2 C.51.1×107km2 D.0.511×109km2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com