
����Ŀ����ͼ��������![]() ��ֱ��
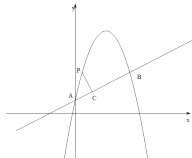
��ֱ��![]() ����A��B���㣬����A��y���ϣ���B�ĺ�����Ϊ4��PΪ��������һ���㣬����P��PC��ֱ��AB������ΪC.
����A��B���㣬����A��y���ϣ���B�ĺ�����Ϊ4��PΪ��������һ���㣬����P��PC��ֱ��AB������ΪC.
��1���������ߵĽ���ʽ��
��2������P��ֱ��AB�Ϸ����������ϣ���P�ĺ�����Ϊm����m�Ĵ���ʽ��ʾ�߶�PC�ij���������߶�PC�����ֵ����ʱ��P������.
��3������P��������������һ�㣬������0�㣼��PAB��45�㡣��ֱ��д����
�ٵ�P�ĺ������ȡֵ��Χ��
��������Ϊ������PΪ���ɵ㡱�����ɵ㡱�ĸ�����

���𰸡���1��![]()
��2��![]() ��
�� ![]()
��3��![]() ��
��![]() 7��.
7��.
�������������������1�����A��B����������������ߵĽ���ʽ���ɽ�����⣮
��2����PF��x����F����AB��E��ֱ��AB��x����D����P��m��-m2+![]() m+1������E��m��
m+1������E��m�� ![]() m+1����PE=-m2+4m���ɡ�PCE�ס�DOA���ɵ�
m+1����PE=-m2+4m���ɡ�PCE�ס�DOA���ɵ�![]() ���������κ����ɽ�����⣮
���������κ����ɽ�����⣮
��3������ͼ2�У�ȡ��F��1��4��������AF��FB������֤����FAB�ǵ���ֱ�������Σ��Ƴ���FAB=45�㣬��ֱ��AF����������P���ɵ�ֱ��AF�Ľ���ʽΪy=3x+1�����÷����������PAB=45��ʱ����P�����꼴�ɽ�����⣬�ٸ��ݶԳ������P��A��PAʱ�ĵ�P������꼴�ɽ�����⣮
�ڹ۲�ͼ���֪��P��������ķ�Χ3��yp��![]() ��-
��-![]() ��yP��3����������ypΪ4��5��6��0��1��2���ֵ�P�ĺ�����
��yP��3����������ypΪ4��5��6��0��1��2���ֵ�P�ĺ�����![]() ��m��4���Ƴ���Ӧ�ĵ�P��7����
��m��4���Ƴ���Ӧ�ĵ�P��7����
�����������1��������A��0��1����B��4��3����
��A��0��1����B��4��3������y=-x2+bx+c�õ�
![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪy=-x2+![]() x+1��
x+1��
��2����PF��x����F����AB��E��ֱ��AB��x����D��
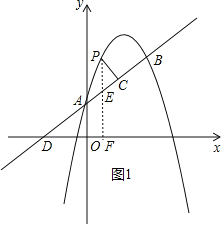
������D��-2��0����A��0��1����
��P��m��-m2+![]() m+1������E��m��
m+1������E��m�� ![]() m+1����PE=-m2+4m
m+1����PE=-m2+4m
��OA=1��OD=2��AD=![]() ��
��
��PF��OA��
���DAO=��DEF=��PEC��
�ߡ�AOD=��PCE=90�㣬
���PCE�ס�DOA��
��![]() ��
��
��![]() ��
��
��PC=-![]() ��m2-4m����
��m2-4m����
��PC=-![]() ��m2-4m��=-
��m2-4m��=-![]() ��m-2��2+
��m-2��2+![]() ��
��
��-![]() ��0��
��0��
��m=2ʱ��PC�����ֵ�����ֵΪ![]() ����ʱP��2��6����
����ʱP��2��6����
��3������ͼ2�У�ȡ��F��1��4��������AF��FB��
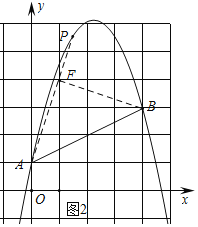
��A��0��1����B��4��3����
��AF=![]() ��FB=
��FB=![]() ��AB=
��AB=![]()
��AF=FB��AF2+BF2=AB2��
���FAB�ǵ���ֱ�������Σ�
���FAB=45������ֱ��AF����������P��
��ֱ��AF�Ľ���ʽΪy=3x+1��
��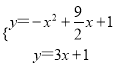
���![]() ��
��![]() ��
��
��A��0��1����
��P��![]() ��
�� ![]() ����
����
��P��A��PAʱ��
ֱ��P��A�Ľ���ʽΪy=-![]() x+1��
x+1��
��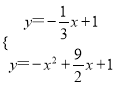 �����
�����![]() ��
��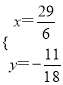 ��
��
��P����![]() ��-
��-![]() ��
��
��۲�ͼ���֪����������0�㣼��PAB��45��ĵ�P�ĺ�����![]() ��m��4��4��m��
��m��4��4��m��![]() ��
��
�ڹ۲�ͼ���֪��P��������ķ�Χ3��yp��![]() ��-
��-![]() ��yP��3
��yP��3
������ypΪ4��5��6��0��1��2���ֵ�P�ĺ�����![]() ��m��4��4��m��
��m��4��4��m��![]() ��
��
���Ӧ�ĵ�P��7����
�ࡰ�ɵ㡱�ĸ���Ϊ7����


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. 33��9B. ��a3��4��a12
C. ��a��b��2��a2��b2D. a2a3��a6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼa�dz�����ֽ������DEF=25�㣬��ֽ����EF�۵���ͼb������BF�۵���ͼc����ͼc�еġ�CFE�Ķ������㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
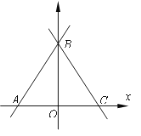
����Ŀ����ͼ��ֱ��y=![]() x��4
x��4![]() ��x�ᡢy��ֱ���A��B���㣬 ��ABC=60�㣬BC��x�ύ�ڵ�C������P��A�������AC���C�˶�������A��C�غϣ���ͬʱ����Q��C�������C��B��A���A�˶�(����C��A�غ�) ������P���˶��ٶ���ÿ��1����λ���ȣ�����Q���˶��ٶ���ÿ��2����λ���ȣ�������APQ��������ʱ��y������һ��M���ڶ������ڴ���һ��N��ʹ��A��Q��M��NΪ������ı���Ϊ����, ���N������Ϊ_________
��x�ᡢy��ֱ���A��B���㣬 ��ABC=60�㣬BC��x�ύ�ڵ�C������P��A�������AC���C�˶�������A��C�غϣ���ͬʱ����Q��C�������C��B��A���A�˶�(����C��A�غ�) ������P���˶��ٶ���ÿ��1����λ���ȣ�����Q���˶��ٶ���ÿ��2����λ���ȣ�������APQ��������ʱ��y������һ��M���ڶ������ڴ���һ��N��ʹ��A��Q��M��NΪ������ı���Ϊ����, ���N������Ϊ_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x1��x2�Ƿ���x2+5x��3��0������������x+x2��x1x2��ֵ�ǣ�������
A. ��8B. 8C. ��2D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
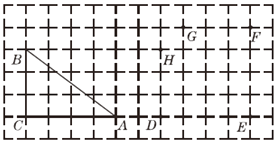
����Ŀ����ͼ��ʾ���ڷ���ֽ�У���ABC���������㼰D��E��F��G��H�����ֱ�λ��С�����εĶ�����.
��1������D��E��F��G��H�е�������Ϊ���㻭�����Σ���������������������ABC��ȫ�ȵ������ȵ��������� ��ֻ��Ҫ��һ�������Σ���
��2���ȴ�D��E������������ȡһ���㣬�ٴ�F��G��H������������ȡ������ͬ�ĵ㣬����ȡ����������Ϊ���㻭�����Σ�����״ͼ����������������ABC�����ȵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ��G20���ݷ����ٿ���ijУ���꼶(1)(2)�������幺��һ��T�����μ�һ��������˽ij�̵�����������T�����Ĵ�����������10��ʱÿ��140Ԫ����������ÿ����1�����ۼ���1Ԫ������������Ϊ60��(��60��)����ʱ��һ��ÿ��80Ԫ��
��1��������� ![]() ��(10��
��(10�� ![]() ��60)��ÿ���ĵ���Ϊ
��60)��ÿ���ĵ���Ϊ ![]() Ԫ����д��
Ԫ����д�� ![]() ����
���� ![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�������(1)(2)�������100��T����������ij��ԭ��������������ҵ�һ������������30��������60������֪��������T����һ������9200Ԫ�����һ��T�����Ĺ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ı߳�Ϊ5��E��BC�����˶���DE���е�G��EG��E˳ʱ����ת90���EF����CEΪ����ʱA��C��F��һ��ֱ���� ��������

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com