
【题目】如图,矩形![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() .
.
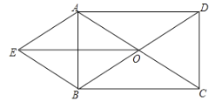
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先证明四边形AOBE是平行四边形,再证明AB⊥OE即可;
(2)根据∠EAO+∠DCO=180°,以及矩形性质可求得∠EAO=120°,求出△AEO面积,利用四边形ADOE的面积等于△AEO面积的2倍即可求解.
(1)∵四边形ABCD是矩形,
∴DO=BO.
∵四边形ADOE是平行四边形,
∴AE∥DO,AE=DO,AD∥OE.
∴AE∥BO,AE=BO,
∴四边形AOBE是平行四边形.
∵AD⊥AB,AD∥OE,
∴AB⊥OE.
∴四边形AOBE是菱形;
(2)设AB与EO交点为M.
∵AB∥CD,
∴∠DCO=∠BAO.
∵四边形AOBE是菱形,
∴∠EAO=2∠BAO.
∵∠EAO+∠DCO=180°,
∴∠EAO=120°,∠EAM=60°.
又AM=![]() AB=
AB=![]() ,
,
∴BM=![]() ,
,
∴MO=![]() ,
,
∴EO=![]()
∴△AEO面积为:![]() ,
,
∴四边形ADOE面积=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
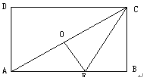
【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
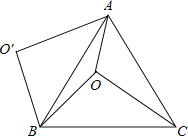
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的正半轴上,直线y=x﹣1交边AB、OA于点D、M,反比例函数![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
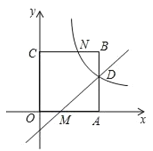
(1)求BN的长.
(2)点P是直线DM上的动点(点P不与点D、点M重合),连接PB、PC、MN,当△BCP的面积等于四边形ABNM的面积时,求点P的坐标.
(3)在(2)的条件下,连接CP,以CP为边作矩形CPEF,使矩形的对角线的交点G落在直线DM上,请写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与x轴负半轴交于B,与正半轴交于点
,与x轴负半轴交于B,与正半轴交于点![]() ,且
,且![]() .
.
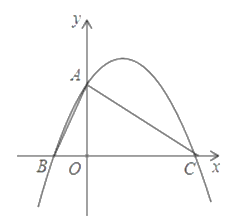
(1)求该二次函数解析式;
(2)若![]() 是线段
是线段![]() 上一动点,作
上一动点,作![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() 当
当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上方的抛物线上的一个动点,连接
轴上方的抛物线上的一个动点,连接![]() ,设所得
,设所得![]() 的面积为
的面积为![]() .问:是否存在一个
.问:是否存在一个![]() 的值,使得相应的点
的值,使得相应的点![]() 有且只有
有且只有![]() 个,若有,求出这个
个,若有,求出这个![]() 的值,并求此时点
的值,并求此时点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
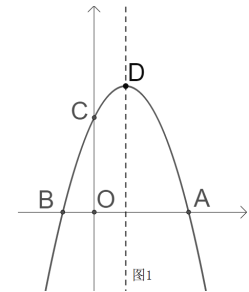
【题目】如图,二次函数![]() 的图象与
的图象与![]() 、
、![]() 轴交于
轴交于![]() 、
、![]() 、
、![]() 三点,其中
三点,其中![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
(1)求![]() 的值及顶点
的值及顶点![]() 的坐标;
的坐标;
(2)如图1,若动点![]() 在第一象限内的抛物线上,动点
在第一象限内的抛物线上,动点![]() 在对称轴
在对称轴![]() 上,当
上,当![]() ,且
,且![]() 时,求此时点
时,求此时点![]() 的坐标;
的坐标;
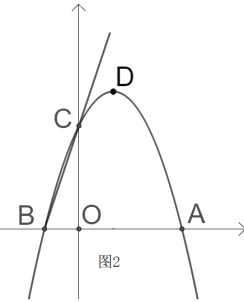
(3)如图2,若点![]() 是二次函数图像上对称轴右侧一点,设点
是二次函数图像上对称轴右侧一点,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,到抛物线的对称轴的距离为
,到抛物线的对称轴的距离为![]() ,当
,当![]() 时,请求出点
时,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场按定价销售某种商品时,每件可获利100元;按定价的八折销售该商品5件与将定价降低50元销售该商品6件所获利润相等.
(1)该商品进价、定价分别是多少?
(2)该商场用10000元的总金额购进该商品,并在五一节期间以定价的七折优惠全部售出,在每售出一件该商品时,均捐献![]() 元给社会福利事业,该商场为能获得不低于3000元的利润,求
元给社会福利事业,该商场为能获得不低于3000元的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
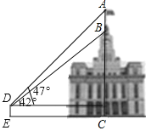
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A、B、C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果精确到0.1m).参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①为了了解一批灯泡的使用寿命,应采用全面调查的方式
②一组数据5,6,7,6, 8,10的众数和中位数都是6
③已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是m≥0
④式子![]() 有意义的条件是
有意义的条件是![]()
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com