
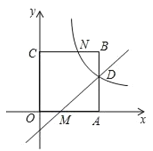
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���C������Ϊ��0��3������A��x����������ϣ�ֱ��y��x��1����AB��OA�ڵ�D��M������������![]() ��ͼ����D����BC�Ľ���ΪN��
��ͼ����D����BC�Ľ���ΪN��
��1����BN�ij���
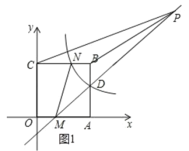
��2����P��ֱ��DM�ϵĶ��㣨��P�����D����M�غϣ�������PB��PC��MN������BCP����������ı���ABNM�����ʱ�����P�����꣮
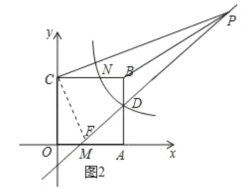
��3���ڣ�2���������£�����CP����CPΪ��������CPEF��ʹ���εĶԽ��ߵĽ���G����ֱ��DM�ϣ���д����G�����꣮
���𰸡���1��1 ��2����7��6�� ��3����![]() ��
��![]() ��
��
��������
��1���������ε����ʿɵó���A��B�����꣬����һ�κ���ͼ���ϵ�����������ɵó���D�����꣬�ɵ�D�����꣬���ô���ϵ�����������������������ʽ�������÷���������ͼ���ϵ�����������ɵó���N�����꣬��ϵ�B����������BN�ij���
��2������һ�κ���ͼ���ϵ�����������ɵó���M�����꣬�������ε������ʽ���������ABNM����������P������Ϊ��x��x-1����x��1��x��3�������������ε������ʽ��ϡ�BCP�������������ABNM����������ɵó�����x�ĺ�����ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
��3������C��CF��CP����DM�ڵ�F�����F������Ϊ��n��n-1������ϵ�C��P�����꣬���������ľ��빫ʽ�����![]() ��ֵ�����ù��ɶ����ɵó�����n��һԪһ�η��̣���֮���ɵó���F�����꣬�ٽ�ϵ�GΪ�߶�PF���е㣬���������G�����꣮
��ֵ�����ù��ɶ����ɵó�����n��һԪһ�η��̣���֮���ɵó���F�����꣬�ٽ�ϵ�GΪ�߶�PF���е㣬���������G�����꣮
�⣺��1��![]() ������OABC
������OABC
![]() ��A��������3��0������B��������3��3����
��A��������3��0������B��������3��3����
![]() ��x��3ʱ��y��x��1��2��
��x��3ʱ��y��x��1��2��
���D��������3��2����
��D��3��2������![]() ���ã�
���ã�![]() ����ã�m��6��
����ã�m��6��
�෴������������ʽΪ![]() ��
��
��y��3ʱ��![]() ����ã�x��2��
����ã�x��2��
���N��������2��3����
��BN��3��2��1��
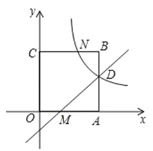
��2����y��0ʱ��x��1��0����ã�x��1��
���M��������1��0����
��AM��2��
![]() ����AMNB
����AMNB![]() ��
��
��ͼ1�����P������Ϊ��x��x��1����x��1��x��3����
![]() ,
,
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
���P��������7��6����
��3������C��CF��CP����DM�ڵ�F��
��ͼ2��ʾ�����F������Ϊ��n��n��1����
�ߵ�C������Ϊ��0��3������P������Ϊ��7��6����
��![]()
![]()
![]()
�ߡ�PCF��90����
��![]() ��
��
��![]()
��ã�![]() ��
��
���F��������![]() ����
����
�֡ߵ�GΪ���ζԽ��ߵĽ��㣬
![]() GΪ�߶�PF���е㣬
GΪ�߶�PF���е㣬
���G��������![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���мƻ������ס���������Ʒ��������Ʒ�Ľ��ۡ��ۼ����±���
��Ʒ | �� | �� |
���ۣ�Ԫ/���� | x60 | x |
�ۼۣ�Ԫ/���� | 200 | 100 |
����1800Ԫ����������Ʒ�ļ�������900Ԫ����������Ʒ�ļ�����ͬ��
��1����ס���������Ʒ�Ľ����Ƕ���Ԫ��
��2�����������ۼס���������Ʒ��100�����������ۼ�����ƷΪa����a40������������100���ס���������Ʒ��������ΪwԪ����w��a֮��ĺ�����ϵʽ�������w����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
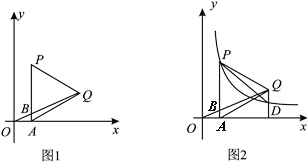
����Ŀ����ͼ1��P��ƽ��ֱ������ϵ�е�һ������һ�㣬����P��PA��x���ڵ�A����APΪ�����Ҳ����ȱ���APQ����֪��Q��������Ϊ2������OQ��AP��B��BQ��3OB��
(1)���P�����ꣻ
(2)��ͼ2��������P��˫����![]() (k��0)�����Q��ֱ��x���ֱ�߽���D������PD����
(k��0)�����Q��ֱ��x���ֱ�߽���D������PD����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ����ѧΪ�˽�����ѧУ��ʫ�ʴ�ᡷ�ϻ�ͬѧ���ƻ�����ס������ֽ�Ʒ��20�������м��ֽ�Ʒÿ��40Ԫ�����ֽ�Ʒÿ��30Ԫ��
��1���������ס������ֽ�Ʒ������650Ԫ����ס������ֽ�Ʒ�������˶��ټ���
��2������������ֽ�Ʒ�ļ������������ֽ�Ʒ������2�����ܻ��Ѳ�����680Ԫ����ѧУ�м��ֲ�ͬ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����дӼ�ȥ��վ���ߵ�6����ʱ����ͬ�����ٶȻؼ�ȡ��Ʒ��Ȼ��Ӽҳ˳��������վ�������Ԥ�Ʋ���ʱ����ǰ��3���ӣ�СԪ���·��S���ף���ʱ��t�����ӣ�֮��ĺ���ͼ����ͼ����ô�Ӽҵ���վ·����___________��
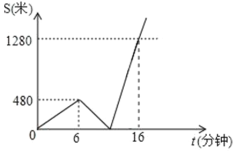
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������λͬѧ����һ��ƹ���������Ҫ����ѡ����λͬѧ���һ������.
��1��������״ͼ�����б�������ǡ��ѡ�мס�����λͬѧ�ĸ���.
��2������ȷ���״��һ�����ٴ�������λͬѧ�����ѡȡһλ����ǡ��ѡ����ͬѧ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У��Խ���
�У��Խ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() Ϊ�ڱ���ƽ���ı���
Ϊ�ڱ���ƽ���ı���![]() ������
������![]() ��
��
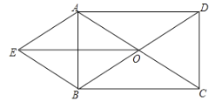
��1����֤���ı���![]() �����Σ�
������
��2����![]() ��
��![]() �����ı���
�����ı���![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
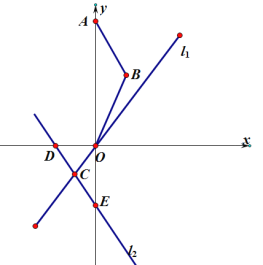
����Ŀ����֪������y=x2+bx+c������A(0,6)����B��1��3����ֱ��l1:y=kx(k��0)��ֱ��l2:y=-x-2��ֱ��l1����������y=x2+bx+c�Ķ���P����l1��l2�ཻ�ڵ�C��ֱ��l2��x�ᡢy��ֱ��ڵ�D��E.��������������ƽ�ƣ�ʹ�����ߵĶ�����ֱ��l2�ϣ���ʱ�����ߵĶ����ΪM�����ٰ�����������ƽ�ƣ�ʹ�����ߵĶ�����ֱ��l1�ϣ���ʱ�����ߵĶ����ΪN����
��1��������y=x2+bx+c�ߵĽ���ʽ��
��2���ж��Ե�NΪԲ�ģ��뾶��Ϊ4��Բ��ֱ��l2��λ�ù�ϵ����˵�����ɣ�
��3�����F��H��ֱ��l1�ϣ���H�ڵ�F���·���������MHF���OAB����ʱ�����F��H�����ֱ꣨��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��Ҫ��ij���������A��B����֮����һ����ֱ�Ĺ�·���ڹ�·���A�����ijũ��C��A�ı�ƫ��68�㷽���ϣ��ڹ�·�յ�B����ø�ũ��c�ڵ�B�ı�ƫ��45�㷽���ϣ���֪A��B�������2400�ף�
��1����ũ��c����·B�ľ��룻���ο����ݣ�sin22���![]() ��cos22���
��cos22���![]() ��tan22���
��tan22���![]() ��
��
��2�������������������Ҫʹ����·���̱�ԭ�ƻ���ǰ4����ɣ��轫�ù���ԭ���Ĺ���Ч�����20%����ԭ�ƻ��ù��̶Ӛ�����·�����ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com