
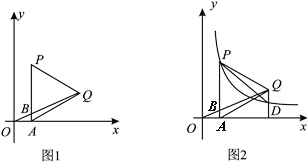
【题目】如图1,P是平面直角坐标系中第一象限内一点,过点P作PA⊥x轴于点A,以AP为边在右侧作等边△APQ,已知点Q的纵坐标为2,连结OQ交AP于B,BQ=3OB.
(1)求点P的坐标;
(2)如图2,若过点P的双曲线![]() (k>0)与过点Q垂直于x轴的直线交于D,连接PD.求
(k>0)与过点Q垂直于x轴的直线交于D,连接PD.求![]() .
.
【答案】(1)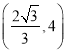 ;(2)
;(2)![]()
【解析】
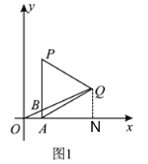
(1)过点Q作x轴的垂线N,根据△APQ是等边三角形及PA⊥x轴得出∠QAN=90°-60°=30°,因为点Q的纵坐标是2,根据解直角三角形可求出AQ与AN的值,根据△AOB∽△ONQ和BQ=3OB可得OA的值,继而可得点P坐标;
(2)设DQ的延长线与过点P平行于x轴的直线交于点E,将P(![]() ,4)代入
,4)代入![]() 可得双曲线解析式,由(1)得D点横坐标,代入解析式即可求出D的纵坐标,即DN的长,从而得到DE的长,在Rt△PED中,PE=AN,
可得双曲线解析式,由(1)得D点横坐标,代入解析式即可求出D的纵坐标,即DN的长,从而得到DE的长,在Rt△PED中,PE=AN,![]() =
=![]() ,将值代入即可求解.
,将值代入即可求解.
解:(1)过点Q作x轴的垂线N
∵△APQ是等边三角形
∴∠PAQ=60°
∵PA⊥x轴
∴∠QAN=90°-60°=30°
∵点Q的纵坐标是2
∴QN=2
∴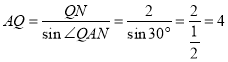
AN=![]() =
=![]() =
=![]()
∴点P纵坐标为4
∵PA⊥x轴,QN⊥x轴
∴△AOB∽△ONQ
∴![]()
∵BQ=3OB
∴![]() =
=![]() =3
=3
∴OA=![]()
∴P点坐标为(![]() ,4).
,4).
故答案为(![]() ,4).
,4).
(2)设DQ的延长线与过点P平行于x轴的直线交于点E

将P(![]() ,4)代入
,4)代入![]() ,得
,得
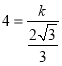
解得k=![]()
∴双曲线解析式为![]()
由(1)知N点横坐标为![]() +
+![]() =
=![]()
即D点横坐标为![]()
∴D点纵坐标为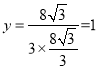
∴DN=1
∴DQ=QN-DN=2-1=1
∴DE=4-1=3
在Rt△PED中,PE=AN=![]()
∴![]() =
=![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
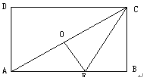
【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
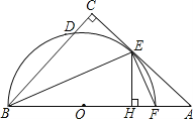
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EF=![]() ,求AF长.
,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.乙回到学校用了______分钟.
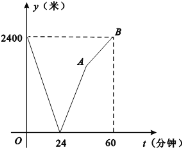
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
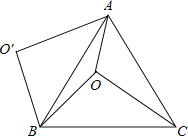
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的正半轴上,直线y=x﹣1交边AB、OA于点D、M,反比例函数![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
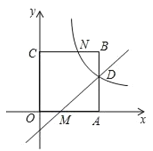
(1)求BN的长.
(2)点P是直线DM上的动点(点P不与点D、点M重合),连接PB、PC、MN,当△BCP的面积等于四边形ABNM的面积时,求点P的坐标.
(3)在(2)的条件下,连接CP,以CP为边作矩形CPEF,使矩形的对角线的交点G落在直线DM上,请写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A、B、C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果精确到0.1m).参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90.
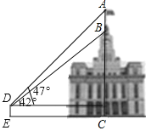
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com