
【题目】已知直线y=kx+b经过点A(5,0),B(1 ,4)
(1)求直线AB的解析式:
(2)若直线y=2x-4与直线AB相交于点C,求点C 的坐标
(3)结合图象,写出关于x的不等式2x- 4≥kx+b的解集,
(4)若直线y=2x-4与x轴交于点D.求△ACD的面积。
【答案】(1)y=-x+5,
(2)(3,2)
(3)x≥3,
(4)3
【解析】
(1)待定系数法求解,
(2)联立函数解析式,组成二元一次方程组求解即可,
(3)作出图像,找到y=-x+5的上方和重合的区域,
(4)利用坐标的几何含义解题.
解:(1)将A(5,0),B(1 ,4)代入y=kx+b中得,
![]() 解得:
解得:![]()
∴y=-x+5,
(2)联立函数解析式得![]() 解得:
解得:![]()
∴C点坐标是(3,2)
(3)作出图像,

由图可知, 2x- 4≥kx+b是取2y=x- 4在y=-x+5的上方和重合的区域,
即x≥3,
(4)令y=2x-4中的y=0,解得x=2,
∴D(2,0)
∴AD=3,C的纵坐标2 是高,
∴S△ADC=![]() =3
=3


科目:初中数学 来源: 题型:
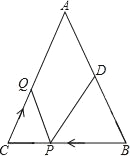
【题目】如图,在△ABC中,∠B=∠C,AB=8,BC=6,点D为AB的中点,点P在线段BC上以每秒2个单位的速度由点B向点C运动,同时点Q在线段CA上以每秒a个单位的速度由点C向点A运动,设运动时间为t(秒)(0≤t≤3).
(1)用含t的代数式表示线段PC的长;
(2)若点P、Q的运动速度相等,t=1时,△BPD与△CQP是否全等,请说明理由.
(3)若点P、Q的运动速度不相等,△BPD与△CQP全等时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
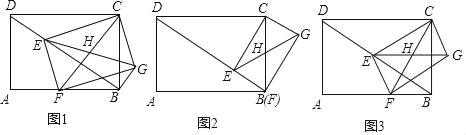
【题目】如图1,矩形ABCD中,AB=8,AD=6;点E是对角线BD上一动点,连接CE,作EF⊥CE交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H.
(1)①如图2,当点F与点B重合时,CE= ,CG= ;
②如图3,当点E是BD中点时,CE= ,CG= ;
(2)在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状?并加以证明;
(3)在图1,![]() 的值是否会发生改变?若不变,求出它的值;若改变,说明理由;
的值是否会发生改变?若不变,求出它的值;若改变,说明理由;
(4)在图1,设DE的长为x,矩形CEFG的面积为S,试求S关于x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EG是⊙O的切线;
(2)若tanC=![]() ,AC=8,求⊙O的半径.
,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,则下列结论:①.AD平分∠BAC;②.△BED≌△FPD;③.DP∥AB;④.DF是PC的垂直平分线.其中正确的是= _________ .(写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.

(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
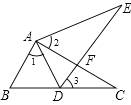
【题目】如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.
求证:△ABC≌△ADE;(填空)
证明:∵∠2+∠E+∠AFE=180° ( )
∠3+∠C+∠CFD=180°(同理)
又∵∠2=∠3( )
∠AFE=∠CFD( )
∴∠E=_________.
∵∠1=∠2(已知)
∴∠1+∠CAD=∠2+∠_______.
即∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为![]() 的AB边上的中点,点前E为AD的中点,
的AB边上的中点,点前E为AD的中点,![]() 为正三角形,给出下列结论,①
为正三角形,给出下列结论,①![]() ,②
,②![]() ,③
,③![]() ,④若
,④若![]() ,点
,点![]() 是
是![]() 上一动点,点
上一动点,点![]() 到
到![]() 、
、![]() 边的距离分别为
边的距离分别为![]() ,
,![]() ,则
,则![]() 的最小值是3.其中正确的结论是_________(填写正确结论的番号)
的最小值是3.其中正确的结论是_________(填写正确结论的番号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com