
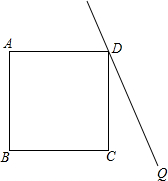
 如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.
如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.分析 (1)根据题意直接画出图形得出即可;
(2)利用对称的性质以及等角对等边进而得出答案;
(3)由轴对称的性质可得:EC=EA,FC=FP,∠DPA=∠DAP=∠DCF,进而利用勾股定理得出答案.
解答 解:(1)如图1所示: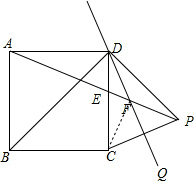
(2)∵∠QDP=∠QDC=25°,DP=DC=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠QDP=∠QDC=25°,
∴∠PDA=140°,
∴∠DPA=$\frac{180°-140°}{2}$=20°;
(3)AE2=EF2+FP2,
∵△DAE≌△DCE,△DFP≌△DFC,
可得:EC=EA,FC=FP,
∠DPA=∠DAP=∠DCF,
∵∠DEA+∠DAP=∠CEF+∠DCF=90°,
∴∠EFC=∠ADC=90°,
∴AE2=EF2+FP2
点评 此题主要考查了正方形的性质以及勾股定理和等腰三角形的性质等知识,利用轴对称的性质得出对应边相等是解题关键.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:填空题
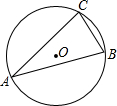 如图,⊙的半径为13cm,若tan∠CAB=$\frac{2}{3}$,那么BC=4$\sqrt{13}$;在本图中,若BC=6,sin∠CAB=$\frac{2}{3}$,那么⊙的半径为9.
如图,⊙的半径为13cm,若tan∠CAB=$\frac{2}{3}$,那么BC=4$\sqrt{13}$;在本图中,若BC=6,sin∠CAB=$\frac{2}{3}$,那么⊙的半径为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com